题目内容
椭圆的左、右焦点分别为![]() 和
和![]() ,且椭圆过点
,且椭圆过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作不与
作不与![]() 轴垂直的直线
轴垂直的直线![]() 交该椭圆于
交该椭圆于![]() 两点,
两点,![]() 为椭圆的左顶点,试判断
为椭圆的左顶点,试判断![]() 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.
解(1)设椭圆方程为![]() ,由题可知:
,由题可知:
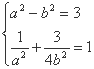 ,解得
,解得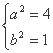 ,所以椭圆的方程
,所以椭圆的方程![]()
(2)设直线![]() 的方程为
的方程为![]() ,联立方程组可得
,联立方程组可得
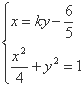 ,化简得:
,化简得:![]()
设![]() ,则
,则![]() ,
,
又![]() ,则
,则
![]() ,
,
所以![]() ,所以
,所以![]() 的大小为定值
的大小为定值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
椭圆的左、右焦点分别为![]() 和
和![]() ,且椭圆过点
,且椭圆过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作不与
作不与![]() 轴垂直的直线
轴垂直的直线![]() 交该椭圆于
交该椭圆于![]() 两点,
两点,![]() 为椭圆的左顶点,试判断
为椭圆的左顶点,试判断![]() 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.
解(1)设椭圆方程为![]() ,由题可知:
,由题可知:
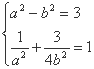 ,解得
,解得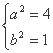 ,所以椭圆的方程
,所以椭圆的方程![]()
(2)设直线![]() 的方程为
的方程为![]() ,联立方程组可得
,联立方程组可得
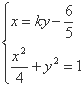 ,化简得:
,化简得:![]()
设![]() ,则
,则![]() ,
,
又![]() ,则
,则
![]() ,
,
所以![]() ,所以
,所以![]() 的大小为定值
的大小为定值

 阅读快车系列答案
阅读快车系列答案