题目内容
已知函数f(x)=(a+1)lnx+ax2+1。
(1)讨论函数f(x)的单调性;
(2)设a<-1,如果对任意x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围。
(1)讨论函数f(x)的单调性;
(2)设a<-1,如果对任意x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围。
解:(1)f(x)的定义域为(0,+∞)
f′(x)=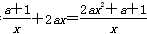
当a≥0时,f′(x)>0,故f(x)在(0,+∞)上单调递增;
当a≤-1时,f′(x)<0,故f(x)在(0,+∞)上单调递减;
当-1<a<0时,令f′(x)=0,解得x=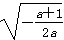
则当x∈(0,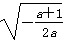 )时,f′(x)>0;
)时,f′(x)>0;
x∈(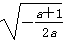 ,+∞)时,f′(x)<0
,+∞)时,f′(x)<0
故f(x)在(0,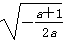 )上单调递增,在(
)上单调递增,在(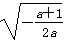 ,+∞)上单调递减。
,+∞)上单调递减。
(2)不妨假设x1≥x2,而a<-1,
由(1)知f(x)在(0,+∞)上单调递减,
从而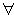 x1,x2∈(0,+∞),
x1,x2∈(0,+∞),
|f(x1)-f(x2)|≥4|x1-x2|等价于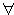 x1,x2∈(0,+∞),f(x2)+4x2≥f(x1)+4x1 ①
x1,x2∈(0,+∞),f(x2)+4x2≥f(x1)+4x1 ①
令g(x)=f(x)+4x,则g′(x)=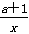 +2ax+4
+2ax+4
①等价于g(x)在(0,+∞)上单调递减,
即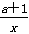 +2ax+4≤0在(0,+∞)上恒成立
+2ax+4≤0在(0,+∞)上恒成立
从而a≤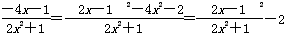
故a的取值范围为(-∞,-2]。
f′(x)=
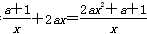
当a≥0时,f′(x)>0,故f(x)在(0,+∞)上单调递增;
当a≤-1时,f′(x)<0,故f(x)在(0,+∞)上单调递减;
当-1<a<0时,令f′(x)=0,解得x=
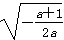
则当x∈(0,
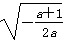 )时,f′(x)>0;
)时,f′(x)>0; x∈(
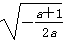 ,+∞)时,f′(x)<0
,+∞)时,f′(x)<0故f(x)在(0,
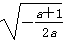 )上单调递增,在(
)上单调递增,在(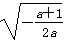 ,+∞)上单调递减。
,+∞)上单调递减。(2)不妨假设x1≥x2,而a<-1,
由(1)知f(x)在(0,+∞)上单调递减,
从而
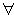 x1,x2∈(0,+∞),
x1,x2∈(0,+∞), |f(x1)-f(x2)|≥4|x1-x2|等价于
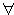 x1,x2∈(0,+∞),f(x2)+4x2≥f(x1)+4x1 ①
x1,x2∈(0,+∞),f(x2)+4x2≥f(x1)+4x1 ①令g(x)=f(x)+4x,则g′(x)=
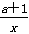 +2ax+4
+2ax+4①等价于g(x)在(0,+∞)上单调递减,
即
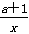 +2ax+4≤0在(0,+∞)上恒成立
+2ax+4≤0在(0,+∞)上恒成立从而a≤
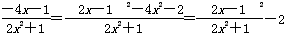
故a的取值范围为(-∞,-2]。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|