题目内容
(本小题满分14分)
设函数f(x)=(x2 +ax+a)e-x,其中x∈R,a是实常数,e是自然对数的底数.
(1)确定a的值,使f(x)的极小值为0;
(2)证明:当且仅当a=5时,f(x)的极大值为5;
(3)讨论关于x的方程![]() 的实数根的个数.
的实数根的个数.
解:(Ⅰ)f ′(x)=(2x+a)e-1-(x2+ax+a) e-1
=- e-1[x2+(a-2)x]
令f ′(x )=0.解得x =0或x =2-a. ……………………………………………………1分
当a=2时,f ′(x)≤0,此时无极值;…………………………………………2分
当0<2-a.即a<2时,f ′(x)和f (x)的变化如下表1:
| x | (-∞,0) | 0 | (0,2- a) | 2- a | (2- a,+∞) |
| f ′(x) | - | 0 | + | 0 | - |
| f (x) | 坨 | 极小值 | 坭 | 极大值 | 坨 |
此时应有f(0)=0,得a =0<2,符合. ……………………………………………3分
③当0>2-a,即a>2时,f ′(x)和f (x)的变化如下表2:
| x | (-∞,2- a) | 2- a | (2- a,0) | 0 | (0,+∞) |
| f ′(x) | - | 0 | + | 0 | - |
| f (x) | 坨 | 极小值 | 坭 | 极大值 | 坨 |
此时应有f(2- a)=0,即[(2- a)2+a(2- a)+a]ea-2=0.
∵e-2≠0. ∴(2- a)2+ a(2- a)+ a =0,得a =4>2,符合……………………………4分
综上,当a =0或a =4时,f (x)的极小值为0. …………………………………………5分
(Ⅱ)若a<2,则由表1可知,应有f(2- a)=5.
即[(2- a)2+a(2- a)+a]ea-2=5,∴(4- a) ea-2=5. ……………………………………6分
设g(a)=(4- a)ea-2,则g ′(a)=- ea-2+(4- a)e-2= e-2(3-a). …………………7分
由a<2.故g ′(a)>0.
∴当a<2时,g(a)<g(2)=2<5,即f(2- a)=5,不可能成立;……………………8分
若a>2,则由表2可知,应有f(0)=5,即a=5.
综上所述,当且仅当a=5时,f (x)的极大值为5. ………………………………………9分
(Ⅲ)∵f (x)=(x2+ax+a)e-1,f ′(x)=- e-1[x2+(a-2)x]
![]() ………………………………10分
………………………………10分
![]() …………………………………11分
…………………………………11分
由渍 ′(x)>0,得x>1;
由渍 ′(x)<0,得x<1,且x≠0.
从而渍 (x)在区间(-∞,0),(0,1)内单调递减;
在区间(1,+∞)内单调递增.………………………………………………………………12分
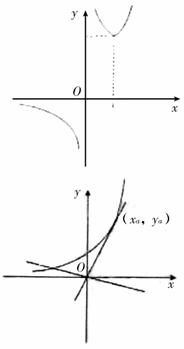 结合函数取值情况,画出如右图所示的草图.
结合函数取值情况,画出如右图所示的草图.
可得当a<0或a=e时,原方程只有一个实数根;
当0≤a<e时,原方程没有实数根;
当a>e时,原方程有两个实数根. …………………14分
(Ⅲ)解法二:∵f (x)=(x2+ax+a)e-1,f ′(x)=- e-1[x2+(a-2)x]
![]()
……………………………………………………………10分
即ax= e-1(x≠0).
考查函数y=ax与y= e2交点个数.如图,可得…………11分
当a<0时,有一个交点;
当a=0时,没有交点. …………………………………12分
当a>0时,若y=ax与y= e2相切,设切点为(x a ,y a),
对y= ex求导,得y′= e′,则a=(ex)′![]() .
.
又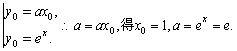
∴当a=e时,有一个交点;
当a>e时,有两个交点. ……………………………………………………………………13分
综上可知:当a<0或a=e时,原方程只有一个实数根;
当0≤a<e时,原方程没有实数根;
当a>e时,原方程有两个实数根. ……………………………………………14分
 www..com
www..com

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)