题目内容
设定义在 上的函数
上的函数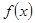 是最小正周期为
是最小正周期为 的偶函数,
的偶函数, 是
是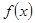 的导函数.当
的导函数.当 时,
时, ;当
;当 且
且 时,
时, .则函数
.则函数 在
在 上的零点个数为 .
上的零点个数为 .

解析试题分析:考查函数 在区间
在区间 上的零点个数情况,即考查函数
上的零点个数情况,即考查函数 与余弦函数的图象在
与余弦函数的图象在 上的公共点个数:当
上的公共点个数:当 且
且 时,由于
时,由于 ,则当
,则当 时,
时, ,
, 令,则函数
令,则函数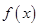 在
在 上单调递增,同理函数
上单调递增,同理函数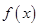 在区间
在区间 上单调递减,又由于函数
上单调递减,又由于函数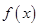 是偶函数,如下图可知,函数
是偶函数,如下图可知,函数 的图象与余弦曲线在区间
的图象与余弦曲线在区间 有且仅有两个公共点,由于函数
有且仅有两个公共点,由于函数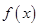 的最小正周期为
的最小正周期为 ,则函数
,则函数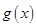 也是以
也是以 为最小正周期的周期函数,故函数
为最小正周期的周期函数,故函数 的图象与余弦曲线在区间
的图象与余弦曲线在区间 、
、 上均有两个公共点,故函数
上均有两个公共点,故函数 的图象与余弦曲线在区间
的图象与余弦曲线在区间 共有
共有 个公共点,故函数
个公共点,故函数 在
在 上的零点个数为
上的零点个数为 .
.
考点:导数、函数的周期性、函数的零点、函数的图象

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 ,
, ,
, ,则
,则 从小到大的顺序为 .
从小到大的顺序为 . 的单调减区间为
的单调减区间为  在点
在点 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,令
,令 ,则
,则 的值为___________.
的值为___________. ,则函数
,则函数 在区间
在区间 上的值域是_____________.
上的值域是_____________. ,则数列中最大项的值为______________。
,则数列中最大项的值为______________。 求
求 .
. =________.
=________. 在点
在点 处的切线平行于
处的切线平行于 轴,则
轴,则 .
.