题目内容
函数f(x)=x2-x-2,x∈[-5,5],在定义域内任取一点x,使f(x)≤0的概率是( )A.

B.

C.

D.

【答案】分析:先解不等式f(x)≤0,得能使事件f(x)≤0发生的x的取值长度为3,再由x总的可能取值,长度为定义域长度10,得事件f(x)≤0发生的概率是0.3
解答:解:∵f(x)≤0?x2-x-2≤0?-1≤x≤2,
∴f(x)≤0?-1≤x≤2,即x∈[-1,2],
∵在定义域内任取一点x,
∴x∈[-5,5],
∴使f(x)≤0的概率P=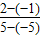 =
=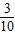
故选C
点评:本题考查了几何概型的意义和求法,将此类概率转化为长度、面积、体积等之比,是解决问题的关键
解答:解:∵f(x)≤0?x2-x-2≤0?-1≤x≤2,
∴f(x)≤0?-1≤x≤2,即x∈[-1,2],
∵在定义域内任取一点x,
∴x∈[-5,5],
∴使f(x)≤0的概率P=
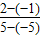 =
=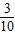
故选C
点评:本题考查了几何概型的意义和求法,将此类概率转化为长度、面积、体积等之比,是解决问题的关键

练习册系列答案
相关题目