题目内容
在△ABC中,a,b,c分别为角A,B,C所对边,若a=2bcosC,则此三角形一定是
- A.等腰直角三角形
- B.直角三角形
- C.等腰三角形
- D.等腰或直角三角形
C
分析:根据a=2bcosC得到bcosC= ,然后根据三角函数定义,得到bcosC=CD=
,然后根据三角函数定义,得到bcosC=CD= ,得到D为BC的中点,根据全等得到三角形ABC为等腰三角形.
,得到D为BC的中点,根据全等得到三角形ABC为等腰三角形.
解答:
解:过A作AD⊥BC,交BC于点D,
在直角三角形ACD中,cosC=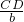 得CD=bcosC,
得CD=bcosC,
而a=2bcosC得bcosC= ,所以CD=
,所以CD=
AD=AD,∠ADB=∠ADC=90°,
BD=CD得到三角形ABD≌三角形ACD,
所以b=c,三角形ABC为等腰三角形.
故选C
点评:考查学生利用三角函数解直角三角形的能力.掌握用全等来证明线段相等的方法.
分析:根据a=2bcosC得到bcosC=
 ,然后根据三角函数定义,得到bcosC=CD=
,然后根据三角函数定义,得到bcosC=CD= ,得到D为BC的中点,根据全等得到三角形ABC为等腰三角形.
,得到D为BC的中点,根据全等得到三角形ABC为等腰三角形.解答:

解:过A作AD⊥BC,交BC于点D,
在直角三角形ACD中,cosC=
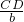 得CD=bcosC,
得CD=bcosC,而a=2bcosC得bcosC=
 ,所以CD=
,所以CD=
AD=AD,∠ADB=∠ADC=90°,
BD=CD得到三角形ABD≌三角形ACD,
所以b=c,三角形ABC为等腰三角形.
故选C
点评:考查学生利用三角函数解直角三角形的能力.掌握用全等来证明线段相等的方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|