题目内容
已知函数f(x)=alnx﹣ax﹣3(a∈R).
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,问:m在什么范围取值时,对于任意的t∈[1,2],函数 在区间(t,3)上总存在极值?
在区间(t,3)上总存在极值?
(Ⅲ)当a=2时,设函数 ,若在区间[1,e]上至少存在一个x0,使得h(x0)>f(x0)成立,试求实数p的取值范围.
,若在区间[1,e]上至少存在一个x0,使得h(x0)>f(x0)成立,试求实数p的取值范围.
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,问:m在什么范围取值时,对于任意的t∈[1,2],函数
 在区间(t,3)上总存在极值?
在区间(t,3)上总存在极值?(Ⅲ)当a=2时,设函数
 ,若在区间[1,e]上至少存在一个x0,使得h(x0)>f(x0)成立,试求实数p的取值范围.
,若在区间[1,e]上至少存在一个x0,使得h(x0)>f(x0)成立,试求实数p的取值范围.解:(Ⅰ)当a=1时,函数f(x)=alnx﹣ax﹣3=lnx﹣x﹣3;导函数为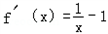 ;
;
当0<x<1时,函数f(x)单调递增,
当时x>1时,函数f(x)单调递减;
故减区间为(1,+∞),增区间为(0,1);
(Ⅱ)由(1,+∞),故g(x)=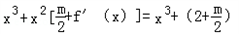 x2-2x,
x2-2x,
g'(x)=3x2+(4+m)x-2,
∵g(x)在区间(t,3)上总存在极值,
∴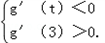
解得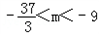 .
.
所以当m在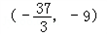 内取值时,对于任意的t∈[{1,2}],
内取值时,对于任意的t∈[{1,2}],
函数 在区间(t,3)上总存在极值.
在区间(t,3)上总存在极值.
(Ⅲ)∴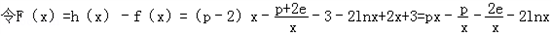
①当p≤0时,由x∈[1,e]得px﹣ ≤0,﹣
≤0,﹣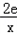 ﹣2lnx<0.
﹣2lnx<0.
所以,在[1,e]上不存在x0,使得h(x0)>f(x0)成立;
②当p>0时,F'(x)=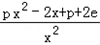 ,∵x∈[1,e],
,∵x∈[1,e],
∴2e﹣2x≥0,px2+p>0,F'(x)>0在[1,e]上恒成立,
故F(x)在[1,e]上单调递增.
∴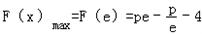 .
.
故只要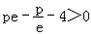 ,,解得
,,解得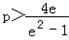 .
.
所以p的取值范围是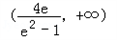 .
.
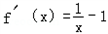 ;
;当0<x<1时,函数f(x)单调递增,
当时x>1时,函数f(x)单调递减;
故减区间为(1,+∞),增区间为(0,1);
(Ⅱ)由(1,+∞),故g(x)=
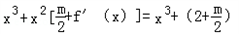 x2-2x,
x2-2x,g'(x)=3x2+(4+m)x-2,
∵g(x)在区间(t,3)上总存在极值,
∴
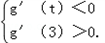
解得
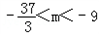 .
.所以当m在
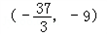 内取值时,对于任意的t∈[{1,2}],
内取值时,对于任意的t∈[{1,2}],函数
 在区间(t,3)上总存在极值.
在区间(t,3)上总存在极值.(Ⅲ)∴
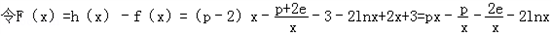
①当p≤0时,由x∈[1,e]得px﹣
 ≤0,﹣
≤0,﹣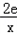 ﹣2lnx<0.
﹣2lnx<0.所以,在[1,e]上不存在x0,使得h(x0)>f(x0)成立;
②当p>0时,F'(x)=
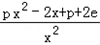 ,∵x∈[1,e],
,∵x∈[1,e],∴2e﹣2x≥0,px2+p>0,F'(x)>0在[1,e]上恒成立,
故F(x)在[1,e]上单调递增.
∴
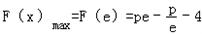 .
.故只要
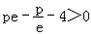 ,,解得
,,解得 .
.所以p的取值范围是
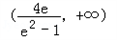 .
.
练习册系列答案
相关题目