Question

在棱长为a的正方体ABCD—A₁B₁C₁D₁中,E、F分别为棱AB和BC的中点,G为上底面A₁B₁C₁D₁的中心.

(1)求AD与BG所成角的余弦值;

(2)求二面角B-FB₁-E的大小;

(3)求点D到平面B₁EF的距离.

Answer 1

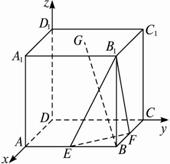
解:建立如图所示的空间直角坐标系D—xyz.?

则A(a,0,0),B(a,a,0),C(0,a,0),E(a,,0),F(,a,0),B₁(a,a,a),G(,,a).

?

(1)∵=(-a,0,0),=(-,-,a),?

∴cos〈,〉===.?

∴AD与BG所成角的余弦值为.                                                                       ?

(2)设平面B₁EF的法向量为n₁=(x,y,z).?

∵=(-,,0),=(0, ,a),?

∴n₁·=0,n₁·=0.?

∴

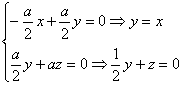
取y=2,则x=2,z=-1.∴可取n₁=(2,2,-1).显然DC⊥平面BFB₁.?

∴可取平面BFB₁的法向量n₂=(0,1,0).?

∴cos〈n₁,n₂〉===.?

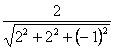∴所求二面角的大小为arccos.                                                                            ?

(3)由(2)已求平面B₁EF的法向量n₁=(2,2,-1),又=(a,a,a),?

∴点D到平面B₁EF的距离D=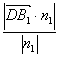==a.?

∴点D到平面B₁EF的距离为a.