题目内容
已知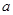 ,
,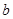 ,
,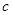 成等差数列且公差不为零,则直线
成等差数列且公差不为零,则直线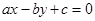 被圆
被圆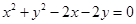 截得的弦长的最小值为_______.
截得的弦长的最小值为_______.
【答案】
2;
【解析】
试题分析: 的圆心为C(1,1),半径为
的圆心为C(1,1),半径为 。
。
因为a,b,c是等差数列,所以有a-2b+c=0,由ax-by+c=0,知直线过定点A(1,2),所以直线 被圆
被圆 截得的弦长的最小值,应是在AC垂直于直线
截得的弦长的最小值,应是在AC垂直于直线 是取到,在弦的一半、半径、圆心到直线的距离构成的直角三角形中,由勾股定理得弦长为2。
是取到,在弦的一半、半径、圆心到直线的距离构成的直角三角形中,由勾股定理得弦长为2。
考点:本题主要考查等差数列的概念,直线与圆的位置关系。
点评:中档题,涉及正弦被圆截得弦长问题,往往借助于弦的一半、半径、圆心到直线的距离构成的直角三角形。

练习册系列答案
相关题目
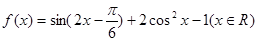
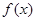 的单调递增区间;
的单调递增区间;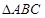 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为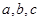 ,已知
,已知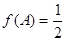 ,
,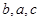 成等差数列,且
成等差数列,且 ,求边
,求边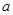 的值.
的值. 成等差数列,
成等差数列, ,
, ,
, 成等比数列,
成等比数列, ,求
,求 .
. (I)求
(I)求 的单调递增区间;(II)在
的单调递增区间;(II)在 中,三内角
中,三内角 的对边分别为
的对边分别为 ,已知,
,已知, 成等差数列,且
成等差数列,且 ,求
,求 的值.
的值.