题目内容
甲、乙两射击运动员分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9,求:
(1)两人都射中的概率;
(2)两人中恰有一人射中的概率;
(3)两人中至少有一人射中的概率.
解:设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B.事件A与B是相互独立的.
(1)两人都射中的概率为P(AB)=P(A)P(B)=0.8×0.9=0.72.
(2)两人中恰有一人射中的概率为 P(A )+P(
)+P( B)=0.8×(1-0.9)+(1-0.8)×0.9=0.26.
B)=0.8×(1-0.9)+(1-0.8)×0.9=0.26.
(3)两人中至少有一人射中的概率等于1减去两个人都没有击中的概率,
∴所求的概率等于 1-P(
 )=1-P(
)=1-P(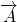 )•P(
)•P( )=1-0.2×0.1=0.98.
)=1-0.2×0.1=0.98.
分析:设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B.
(1)两人都射中的概率为P(AB)=P(A)P(B),运算求得结果.
(2)两人中恰有一人射中的概率为 P(A )+P(
)+P( B)=0.8×(1-0.9)+(1-0.8)×0.9,运算求得结果.
B)=0.8×(1-0.9)+(1-0.8)×0.9,运算求得结果.
(3)两人中至少有一人射中的概率等于1减去两个人都没有击中的概率,即 1-P(
 )=1-P(
)=1-P(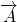 )•P(
)•P( ),运算求得结果.
),运算求得结果.
点评:本题主要考查相互独立事件的概率乘法公式,以及互斥事件的概率加法公式的应用,所求的事件与它的对立事件概率间的关系,属于基础题.
(1)两人都射中的概率为P(AB)=P(A)P(B)=0.8×0.9=0.72.
(2)两人中恰有一人射中的概率为 P(A
 )+P(
)+P( B)=0.8×(1-0.9)+(1-0.8)×0.9=0.26.
B)=0.8×(1-0.9)+(1-0.8)×0.9=0.26.(3)两人中至少有一人射中的概率等于1减去两个人都没有击中的概率,
∴所求的概率等于 1-P(

 )=1-P(
)=1-P(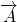 )•P(
)•P( )=1-0.2×0.1=0.98.
)=1-0.2×0.1=0.98.分析:设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B.
(1)两人都射中的概率为P(AB)=P(A)P(B),运算求得结果.
(2)两人中恰有一人射中的概率为 P(A
 )+P(
)+P( B)=0.8×(1-0.9)+(1-0.8)×0.9,运算求得结果.
B)=0.8×(1-0.9)+(1-0.8)×0.9,运算求得结果.(3)两人中至少有一人射中的概率等于1减去两个人都没有击中的概率,即 1-P(

 )=1-P(
)=1-P(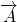 )•P(
)•P( ),运算求得结果.
),运算求得结果.点评:本题主要考查相互独立事件的概率乘法公式,以及互斥事件的概率加法公式的应用,所求的事件与它的对立事件概率间的关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,x(x>
,x(x>
 ,x(x>
,x(x>