题目内容
设 ,
, ,
,
(1)求f(x)的最小正周期、最大值及f(x)取最大值时x的集合;
(2)若锐角α满足
 ,求
,求 的值.
的值.
【答案】分析:(1)由数量积的定义和三角函数的化简方法可得f(x)= ,由三角函数的知识可得所求;(2)由
,由三角函数的知识可得所求;(2)由 得
得 ,结合范围可得
,结合范围可得 ,代入可得所求.
,代入可得所求.
解答:解:(1)由题意可得 …(1分)
…(1分)
= =
=
= …(3分)
…(3分)
= …(4分)
…(4分)
故最小正周期 …(5分)
…(5分)
当 ,即
,即 时,f(x)有最大值
时,f(x)有最大值 ,
,
此时,所求x的集合为 .…(7分)
.…(7分)
(2)由 得
得  ,故
,故 …(9分)
…(9分)
又由 得
得  ,故
,故 ,解得
,解得 .…(11分)
.…(11分)
从而 . …(12分)
. …(12分)
点评:本题考查平面向量数量积的运算,涉及三角函数的运算,属中档题.
 ,由三角函数的知识可得所求;(2)由
,由三角函数的知识可得所求;(2)由 得
得 ,结合范围可得
,结合范围可得 ,代入可得所求.
,代入可得所求.解答:解:(1)由题意可得
 …(1分)
…(1分)=
 =
=
=
 …(3分)
…(3分)=
 …(4分)
…(4分) 故最小正周期
 …(5分)
…(5分)当
 ,即
,即 时,f(x)有最大值
时,f(x)有最大值 ,
,此时,所求x的集合为
 .…(7分)
.…(7分)(2)由
 得
得  ,故
,故 …(9分)
…(9分)又由
 得
得  ,故
,故 ,解得
,解得 .…(11分)
.…(11分)从而
 . …(12分)
. …(12分)点评:本题考查平面向量数量积的运算,涉及三角函数的运算,属中档题.

练习册系列答案
相关题目
 .
. ,求b值.
,求b值.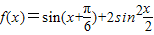 .
. ,求b值.
,求b值. .
. ,c=3,求a的值.
,c=3,求a的值. .
. ,求b值.
,求b值.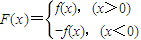 .
.