题目内容
已知α,β∈(0,π),且tanα=2,cosβ=- .
.
(1)求cos2α的值;
(2)求2α-β的值.
解:(1)cos2α=cos2α-sin2α= =
= ,
,
因为tanα=2,所以 ,
,
所以cos2α=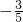 .
.
(2)因为α∈(0,π),且tanα=2,所以
又cos2α=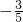 ,∴
,∴ ,
, ,
,
因为β∈(0,π),cosβ=- .
.
所以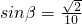 ,
,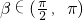 ,
,
所以sin(2α-β)=sin2αcosβ-cos2αsinβ
=
=- ,
,
又 ,
,
∴2α-β=- .
.
分析:(1)利用二倍角的余弦函数,通过分母“1=sin2α+cos2α”的代换,然后化简分式2tanα的形式,代入数值全家健康.
(2)通过α,β的范围求出sin2α,sinβ,通过二倍角的正弦函数,求出sin(2α-β)的值,结合角的范围求出角的大小即可.
点评:本题考查同角三角函数的基本关系式,二倍角的余弦函数与两角和与差的三角函数的应用,考查计算能力,注意角的范围是解题的关键.
 =
= ,
,因为tanα=2,所以
 ,
,所以cos2α=
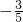 .
.(2)因为α∈(0,π),且tanα=2,所以

又cos2α=
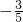 ,∴
,∴ ,
, ,
,因为β∈(0,π),cosβ=-
 .
.所以
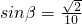 ,
,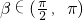 ,
,所以sin(2α-β)=sin2αcosβ-cos2αsinβ
=

=-
 ,
,又
 ,
,∴2α-β=-
 .
.分析:(1)利用二倍角的余弦函数,通过分母“1=sin2α+cos2α”的代换,然后化简分式2tanα的形式,代入数值全家健康.
(2)通过α,β的范围求出sin2α,sinβ,通过二倍角的正弦函数,求出sin(2α-β)的值,结合角的范围求出角的大小即可.
点评:本题考查同角三角函数的基本关系式,二倍角的余弦函数与两角和与差的三角函数的应用,考查计算能力,注意角的范围是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.
如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.