题目内容
设双曲线的焦点在x轴上，两条渐近线为y=±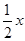
，则该双曲线的离心率e为（ ）
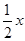，则该双曲线的离心率e为（ ）| A．5 | B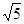． | C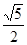． | D． |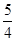
C
分析：设双曲线方程为
- 
=1（a＞0，b＞0），由双曲线渐近线方程得a=2b，根据平方关系，得c= 
= 
b，最后用离心率的公式，可算出该双曲线的离心率．解：∵双曲线焦点在x轴，
∴设双曲线方程为
- =1，a＞0且b＞0∵双曲线的渐近线方程为y=±
x，∴
=，得a=2b由此可得：c=
= b∴双曲线的离心率为e=
=
=
故选：C
练习册系列答案
名校课堂系列答案
相关题目
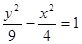的渐近线方程是 ． 
（a＞0，b＞0）的两焦点，以线段F1F2为边作正三角形MF1F2，若边MF1的中点在双曲线上，则双曲线的离心率是 （ ） 
+1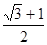 
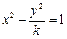的焦点到渐近线的距离为
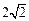，则实数k的值是 
＝
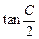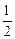，则过点C，以A，H为焦点的双曲线的离心率为 ．
的距离之和为4，则曲线C的方程是 
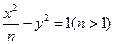的两个焦点为
，
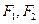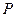在双曲线上，且满足
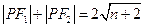，则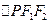
的面积为 （ ）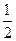
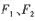分别是双曲线
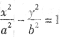的左、右焦点，过F1且垂直于X轴的直线与双曲线交于A,B两点，若
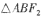为钝角三角形,则该双曲线的离心率e的取值范围是
)
)
•)
)
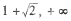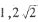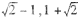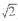的渐近线方程为
，则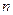
= ．