题目内容
椭圆T的中心为坐标原点O,右焦点为F(2,0),且椭圆T过点E(2,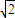 ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.(1)求椭圆T的方程;
(2)设△ABC的三条边所在直线的斜率分别为k1,k2,k3,且ki≠0,i=1,2,3.若直线OM,ON,OP的斜率之和为0,求证:
 为定值.
为定值.
【答案】分析:(1)设出椭圆的标准方程,利用椭圆的定义,即可确定椭圆的标准方程;
(2)利用点差法,确定三条边所在直线的斜率,结合直线OM,ON,OP的斜率之和为0,即可得到结论.
解答:解:(1)设椭圆T的方程为 (a>b>0),
(a>b>0),
由题意知:左焦点为F′(-2,0),所以2a=|EF|+|EF′|= +3
+3 ,
,
解得a=2 ,
,
∵c=2,∴ =2.
=2.
故椭圆T的方程为 …(4分)
…(4分)
(2)设A(x1,y1),B(x2,y2),C(x3,y3),M(s1,t1),N(s2,t2),P(s3,t3),
由: ,
, ,两式相减,得到
,两式相减,得到
(x1-x2)(x1+x2)+2(y1-y2)(y1+y2)=0
所以 =
= ,即
,即 ,…(9分)
,…(9分)
同理 ,
,
所以 ,
,
又因为直线OM,ON,OP的斜率之和为0,
所以 =0 …(13分)
=0 …(13分)
点评:本题考查椭圆的标准方程,考查点差法的运用,考查学生的计算能力,属于中档题.
(2)利用点差法,确定三条边所在直线的斜率,结合直线OM,ON,OP的斜率之和为0,即可得到结论.
解答:解:(1)设椭圆T的方程为
 (a>b>0),
(a>b>0),由题意知:左焦点为F′(-2,0),所以2a=|EF|+|EF′|=
 +3
+3 ,
,解得a=2
 ,
,∵c=2,∴
 =2.
=2.故椭圆T的方程为
 …(4分)
…(4分)(2)设A(x1,y1),B(x2,y2),C(x3,y3),M(s1,t1),N(s2,t2),P(s3,t3),
由:
 ,
, ,两式相减,得到
,两式相减,得到(x1-x2)(x1+x2)+2(y1-y2)(y1+y2)=0
所以
 =
= ,即
,即 ,…(9分)
,…(9分)同理
 ,
,
所以
 ,
,又因为直线OM,ON,OP的斜率之和为0,
所以
 =0 …(13分)
=0 …(13分)点评:本题考查椭圆的标准方程,考查点差法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.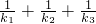 为定值.
为定值. ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P. 为定值.
为定值. ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P. 为定值.
为定值.