题目内容
【题目】如图，正四面体A﹣BCD的棱长为a，点E、F分别是棱BD、BC的中点，则平面AEF截该正四面体的内切球所得截面的面积为_____.
【答案】
【解析】
设圆心为P，内切球的球心为O,内切球的半径为r，作
平面
,则
为底面三角形的中心,由OP⊥AM，
可得,
,利用相似比
求出
,利用四面体中的几何关系求出r，再由截面圆的性质可知,所求截面圆的半径
求解即可.
作图如下:
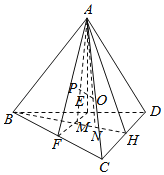
根据题意知,平面AEF截该正四面体的内切球所得截面一定是圆，
设圆心为P，内切球的球心为O，
作平面,则为底面三角形的中心,
在等边三角形中,
,
在
中,由勾股定理知,
,
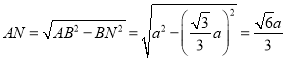由图可知,
为四面体外接球的半径,设
,
在
中,由勾股定理可得,
,解得
，
所以正四面体A﹣BCD的内切球半径为
,
因为OP⊥AM，,所以，
又因为
，
由AM2＝NM2+AN2可得AM
，
所以，即
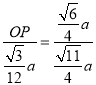,解得OP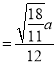
，
∴平面AEF截该正四面体的内切球所得截面圆半径r1
，
平面AEF截该正四面体的内切球所得截面的面积为
，
故答案为:
练习册系列答案
相关题目
