题目内容
已知长轴在x轴上的椭圆的离心率e=
，且过点P（1，1）．
（1）求椭圆的方程；
（2）若点A（x0，y0）为圆x2+y2=1上任一点，过点A作圆的切线交椭圆于B，C两点，求证：CO⊥OB（O为坐标原点）．
| ||
| 3 |
（1）求椭圆的方程；
（2）若点A（x0，y0）为圆x2+y2=1上任一点，过点A作圆的切线交椭圆于B，C两点，求证：CO⊥OB（O为坐标原点）．
（1）由题意，设椭圆方程为
+
=1(a＞b＞0)
∵e=
，∴
=
，∴a2=3b2
∵椭圆过点P（1，1），∴
+
=1
∴a2=4，b2=
∴椭圆的方程为
+
=1；
（2）证明：由题意可求得切线方程为x0x+y0y=1
①若y0=0，则切线为x=1（或x=-1），则B（1，1），C（1，-1），∴CO⊥OB（当x=-1时同理可得）；
②当y0≠0时，切线方程为x0x+y0y=1，与椭圆联立并化简得(3x02+y02)x2-6x0x+3-4y02=0
∴x1+x2=
，x1x2=
设B（x1，y1），C（x2，y2），则x1x2+y1y2=(1+
)x1x2-
(x1+x2)+
=(1+
)×
-
×
+
=0
∴CO⊥OB
| x2 |
| a2 |
| y2 |
| b2 |
∵e=
| ||
| 3 |
| a2-b2 |
| a2 |
| 2 |
| 3 |
∵椭圆过点P（1，1），∴
| 1 |
| a2 |
| 1 |
| b2 |
∴a2=4，b2=
| 4 |
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
| 3y2 |
| 4 |
（2）证明：由题意可求得切线方程为x0x+y0y=1
①若y0=0，则切线为x=1（或x=-1），则B（1，1），C（1，-1），∴CO⊥OB（当x=-1时同理可得）；
②当y0≠0时，切线方程为x0x+y0y=1，与椭圆联立并化简得(3x02+y02)x2-6x0x+3-4y02=0
∴x1+x2=
| 6x0 |
| 3x02+y02 |
| 3-4y02 |
| 3x02+y02 |
设B（x1，y1），C（x2，y2），则x1x2+y1y2=(1+
| x02 |
| y02 |
| x0 |
| y02 |
| 1 |
| y02 |
=(1+
| x02 |
| y02 |
| 3-4y02 |
| 3x02+y02 |
| x0 |
| y02 |
| 6x0 |
| 3x02+y02 |
| 1 |
| y02 |
∴CO⊥OB
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
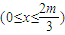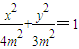
和椭圆弧
和椭圆弧
