��Ŀ����
����Ŀ��Ϊ�˽ⴺ����ҹ�²��С��ij���ӷ�ѿ����֮��Ĺ�ϵ�����ڴ�4�·ݵ�30���������ѡ��5������о����ҷֱ��¼��ÿ����ҹ�²���ÿ��100�����ӽ��ݺ�ķ�ѿ�����õ��������ϣ�
���� | 4��1�� | 4��7�� | 4��15�� | 4��21�� | 4��30�� |
�²�x/�� | 10 | 11 | 13 | 12 | 8 |
��ѿ��y/�� | 23 | 25 | 30 | 26 | 16 |
������5������ѡ2�죬�Ƿ�ѿ���������ֱ�Ϊm��n�����¼���m��n����С��25���ĸ��ʣ�
������5������ѡ2�죬��ѡȡ����4��1����4��30�յ��������ݣ��������5���е���3������ݣ����y����x�����Իع鷽�� ![]() =
= ![]() x+
x+ ![]() ��
��
���ο���ʽ�� ![]() =
=  ��
�� ![]() =
= ![]() ��
�� ![]()
![]() ��
��
���𰸡��⣺���������飨m��n����ʾѡ��2��ķ�ѿ����� m��n������ȡֵ����У�
��23��25������23��30������23��26������23��16������25��30����
��25��26������25��16������30��26������30��16������30��26��������10��
�衰m��n����С��25��Ϊ�¼�A��
������Ļ����¼��У�25��30������25��26������30��26��
����P��A��= ![]() ��
��
��m��n����С��25�ĸ���Ϊ ![]() ��
��
���������ݵ� ![]() =12��
=12�� ![]() =27��3
=27��3 ![]()
![]() =972��
=972�� ![]() xiyi=977��
xiyi=977�� ![]() xi2=434��3
xi2=434��3 ![]() 2=432��
2=432��
�ɹ�ʽ���� ![]() =
= ![]() =
= ![]() ��
�� ![]() =27��
=27�� ![]() ��12=��3��
��12=��3��
����y����x�����Իع鷽��Ϊ ![]() =
= ![]() x��3
x��3
�����������������飨m��n����ʾѡ��2��ķ�ѿ��������оٷ��ɵ�m��n������ȡֵ����������ɵ�m��n����С��25�������Ŀ���ɹŵ����ʽ������ɵô𰸣����������������ݣ�������x��y��ƽ�������������������ݵ��������ĵ㣬������С���˷�������Իع鷽�̵�ϵ����д�����Իع鷽�̣�

����Ŀ����У�߶��꼶��2000��ѧ������������1200��.Ϊ����ѧ���ǵ��ֻ�ʹ����������÷ֲ�����ķ����������ȡ100λѧ��ÿ��ƽ��ʹ���ֻ�����ʱ����������ݣ���λ��Сʱ��.������100�����ݣ��õ�ѧ��ÿ��ƽ��ʹ���ֻ�����ʱ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���������������ݷ�������ֱ�Ϊ![]() .
.
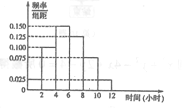
��1��Ӧ�ռ�������Ů���������ݸ������ˣ�
��2��������У�߶��꼶ѧ��ÿ��ƽ��ʹ���ֻ�����ʱ�䳬��4Сʱ�ĸ���.
��3����ƽ��ÿ��ʹ���ֻ�����ʱ����![]() �ڶ���Ϊ����ʱ��ʹ���ֻ�������
�ڶ���Ϊ����ʱ��ʹ���ֻ�������![]() �ڶ���Ϊ����ʱ��ʹ���ֻ���.�����������У���25��ѧ��������.���������2��2�����������ж��Ƿ���99.5%�İ�����Ϊ��ѧ��ÿ��ʹ���ֻ�����ʱ������ӳ̶��йء�.
�ڶ���Ϊ����ʱ��ʹ���ֻ���.�����������У���25��ѧ��������.���������2��2�����������ж��Ƿ���99.5%�İ�����Ϊ��ѧ��ÿ��ʹ���ֻ�����ʱ������ӳ̶��йء�.
���� | ������ | �ϼ� | |
��ʱ��ʹ���ֻ����� | |||
��ʱ��ʹ���ֻ����� | 15 | ||
�ϼ� | 25 |
����![]()
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 6.635 | 7.879 |