Question

已知函数f（x）=．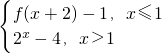
（1）求f（-3）的值；
（2）A={x|-1＜x≤4}，B={x|f（x）≤3}，求A∩B．

Answer 1

解：（1）由已知可得，f（-3）=f（-3+2）-1=f（-1）-1=f（-1+2）-2
=f（1）-2=f（1+2）-3=f（3）-3=2³-4-3=1；
（2）当x＞1时，由f（x）≤3可得2^x-4≤3可得B={x|1＜x≤log₂7}
此时A∩B={x|1＜x≤log₂7}
当x≤1时，要求A∩B，结合A中的x的范围，只需考虑集合B中的-1＜x≤1，1＜x+2≤3
此时，f（x）=f（x+2）-1=2^x+2-5≤3，解可得-1＜x≤1
此时A∩B={x|-1＜x≤1}
∴A∩B={x|-1＜x≤log₂7}
分析：（1）根据分段函数的对应关系，直接代入求解
（2）要求集合B，需要知道f（x），对x的范围分x＞1时，由f（x）≤3可得，2^x-4≤3可得；x≤1时，要求A∩B，结合A中的x的范围，只需考虑集合B中的-1＜x≤1，1＜x+2≤3，f（x）=f（x+2）-1=2^x+2-5≤3，从而可求
点评：本题主要考查了分段函数的函数值的求解及不等式的解法，求解的关键是要根据不同的变量，确定不同的对应关系，（2）解不等式时，当x≤1时，函数的解析式不容易求出，本题的解法中涉及到的解题的技巧要注意体会掌握．