题目内容
14.已知抛物线y2=2px(p>0)上一点M(1,m)到其焦点的距离为5,则该抛物线的准线方程为x=-4.分析 由题意得:抛物线焦点为F($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$.因为点M(1,m)到其焦点的距离为5,所以点M到抛物线的准线的距离为:1+$\frac{p}{2}$=5,从而得到p=8,得到该抛物线的准线方程.
解答 解:∵抛物线方程为y2=2px
∴抛物线焦点为F($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$
又∵点M(1,m)到其焦点的距离为5,
∴p>0,根据抛物线的定义,得1+$\frac{p}{2}$=5,
∴p=8,∴准线方程为x=-4.
故答案为:x=-4.
点评 本题给出一个特殊的抛物线,在已知其上一点到焦点距离的情况下,求准线方程.着重考查了抛物线的定义和标准方程,以及抛物线的基本概念,属于基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
4.已知集合D={x|$\frac{24-x}{x-9}$>0},若a,b∈D,且$\frac{1}{a}$+$\frac{1}{2b}$=$\frac{1}{12}$,则9a•3b的最小值为354.
5.将四名青年志愿者安排到三个社区参加劳动,要求每个社区至少安排一名,则不同的安排方法种数是( )
| A. | 72 | B. | 36 | C. | 24 | D. | 12 |
3.己知等差数列{an}的首项为a1,公差为d,其前n项和为Sn,若直线y=a1x与圆(x-1)2+y2=1的两个交点关于直线x+y+d=0对称,则Sn=( )
| A. | n2 | B. | -n2 | C. | $\frac{-{n}^{2}+3n}{2}$ | D. | n2-2n |
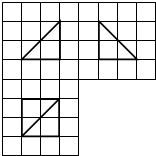 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的表面积为12π.
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的表面积为12π.