题目内容
已知函数y=(sinx+cosx)2+2cos2x,则它的最大值为( )
A.
| B.
| C.
| D.
|
函数y=(sinx+cosx)2+2cos2x
=sin2x+cos2x+2sinxcosx+cos2x+1
=2+sin2x+cos2x
=2+
sin(2x+
),
∵x∈R,∴-1≤sin(2x+
)≤1,
则函数的最大值为2+
.
故选D
=sin2x+cos2x+2sinxcosx+cos2x+1
=2+sin2x+cos2x
=2+
| 2 |
| π |
| 4 |
∵x∈R,∴-1≤sin(2x+
| π |
| 4 |
则函数的最大值为2+
| 2 |
故选D

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
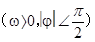 的部分图象如图所( )
的部分图象如图所( )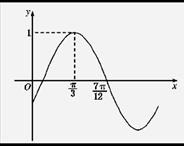
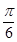 B.ω=1,φ=-
B.ω=1,φ=-