题目内容
4.设函数f(x)=alnx+$\frac{2{a}^{2}}{x}$(a≠0).(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若a=1,求证:对于定义域内的任意一个x,都有f(x)≥3-x.
分析 (Ⅰ)先求出函数的导数,再根据a的范围,求出函数的单调区间;
(Ⅱ)a=1时,f(x)=lnx+$\frac{2}{x}$,定义域是x>0,设F(x)=f(x)-(3-x)=lnx+x+$\frac{2}{x}$-3,由F(x)min=F(1)=0,能够证明f(x)≥3-x.
解答 解:(Ⅰ)∵f(x)=a1nx+$\frac{{2a}^{2}}{x}$(a≠0),
∴f′(x)=$\frac{a}{x}$-$\frac{{2a}^{2}}{{x}^{2}}$=$\frac{a(x-2a)}{{x}^{2}}$,
①当a>0时,由f′(x)>0得,x>2a;由f′(x)<0得,x<2a.
∴f(x)(a≠0)的增区间是(2a,+∞),减区间是(0,2a).
②当a<0时,由f′(x)<0恒成立,故f(x)(a≠0)在(0,+∞)递减;
(Ⅱ)证明:a=1时,f(x)=lnx+$\frac{2}{x}$,定义域是x>0,
设F(x)=f(x)-(3-x)=lnx+x+$\frac{2}{x}$-3,
F′(x)=$\frac{1}{x}$+1-$\frac{2}{{x}^{2}}$=$\frac{{x}^{2}+x-2}{{x}^{2}}$=0,
x2+x-2=0
∴x=1,x=-2(舍去)
当F′(x)>0时,x>1;
当F′(x)=0时,x=1;
当F′(x)<0时,x>1.
∴F(x)min=F(1)=0+1+2-3=0
∴F(x)≥0,
∴f(x)≥3-x.
点评 本题考查不等式的证明,考查函数的单调性的讨论,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化,合理地运用导数知识解题.

练习册系列答案
相关题目
15.因为对数函数y=logax是增函数(大前提),而是对数函数$y={log_{\frac{1}{3}}}x$(小前提),所以y=log${\;}_{\frac{1}{3}}$x是增函数(结论).这个推理过程中( )
| A. | 大前提错误导致结论错误 | |
| B. | 小前提错误导致结论错误 | |
| C. | 推理形式错误导致结论错误 | |
| D. | 大前提和小前提都错误导致结论错误 |
9.执行如图所示的程序框图,若输出S的值为$\frac{2014}{2015}$,则判断框内可填入的条件是( )
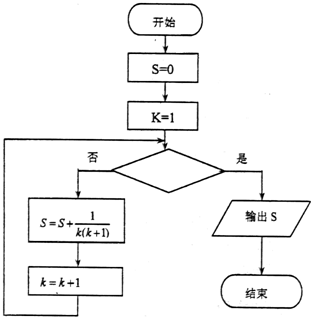

| A. | k>2013 | B. | k>2014 | C. | k>2015 | D. | k>2016 |
13.已知离散型随机变量X的分布列为P(X=1)=$\frac{3}{5}$,P(X=2)=$\frac{3}{10}$,P(X=3)=$\frac{1}{10}$,则X的数学期望E(X)=( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
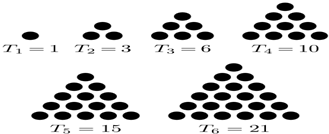 小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.
小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.