题目内容
(本大题14分)
已知函数 定义域为
定义域为 ,且满足
,且满足 .
.
(Ⅰ)求 解析式及最小值;
解析式及最小值;
(Ⅱ)求证: ,
, 。
。
(Ⅲ)设 。求证:
。求证: ,
, .
.
【答案】
(1) ,
,
(2)见解析;(3)
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)求解导数,然后判定单调性,然后分析最值。
(2)求解导数可知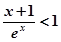
(3)构造函数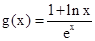 ,利用导数分析最值,进而证明不等式。
,利用导数分析最值,进而证明不等式。
解:(1) ,
,
(2)求导可知: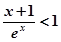
(3) ,
,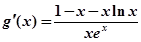
故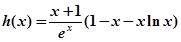 ,令
,令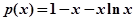
求导易知 最大值为
最大值为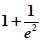 ,而
,而 ,且
,且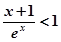
故

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
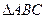 中,
中,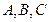 的对边分别为
的对边分别为 ,且
,且 ,
, 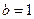 .(1)若
.(1)若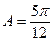 ,求边
,求边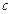 的大小; (2)求
的大小; (2)求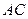 边上高的最大值.
边上高的最大值. 的一个顶点为
的一个顶点为 ,离心率
,离心率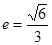 .
. ,
, 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 对任意的
对任意的 成立,则称函数
成立,则称函数 上的“k阶收缩函数”
上的“k阶收缩函数” ,试写出
,试写出 ,
, 的表达式;
的表达式; 试判断
试判断 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与 的关系式;
的关系式; 的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3