题目内容
已知函数f（x）=Asin（3x+ρ）（A＞0，x∈（-∞，+∞），0＜ρ＜π）在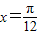
时取得最大值4．（1）求f（x）的最小正周期；
（2）求f（x）的解析式；
（3）若
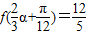，求sinα．
【答案】分析：（1）根据T=
可直接得到答案．
（2）先根据最大值求出振幅A的值，再由
时取得最大值可求出ρ的值，进而可得到函数f（x）的解析式．
（3）根据
，求出cos2α的值，最后根据二倍角公式得到sinα的值．
解答：解：（1）由周期计算公式，可得T=
（2）由f（x）的最大值是4知，A=4
，即sin（
）=1
∵0＜ρ＜π，∴
∴
，∴
∴f（x）=4sin（3x+
）
（3）f（
）=4sin[3（
）+
]=
，即sin[3（
）+
]=
，
，
，
，
．
点评：本题主要考查二倍角公式的应用和正弦函数的基本性质--周期和最值．属基础题．
可直接得到答案．（2）先根据最大值求出振幅A的值，再由
时取得最大值可求出ρ的值，进而可得到函数f（x）的解析式．（3）根据
，求出cos2α的值，最后根据二倍角公式得到sinα的值．解答：解：（1）由周期计算公式，可得T=
（2）由f（x）的最大值是4知，A=4
，即sin（）=1∵0＜ρ＜π，∴
∴，∴∴f（x）=4sin（3x+
）（3）f（
）=4sin[3（）+]=，即sin[3（）+]=，，，，．点评：本题主要考查二倍角公式的应用和正弦函数的基本性质--周期和最值．属基础题．
练习册系列答案
相关题目