题目内容
已知函数f（x）=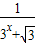
，（1）f（0）+f（1），f（-1）+f（2），f（-2）+f（3）的值；
（2）归纳猜想一般性的结论，并证明之．
【答案】分析：由f（x）计算各和式，得出结论然后归纳猜想，再证明一般性结论．
解答：解：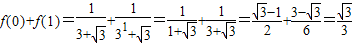
，
同理可得：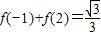
，
．
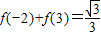证明：设x1+x2=1，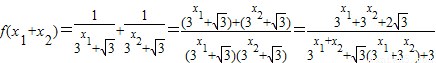
=
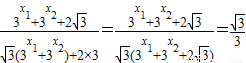
点评：本题主要考查归纳推理，一般思路是从具体到一般，得到一般性结论，然后再证明．属中档题．
解答：解：
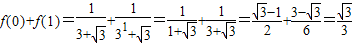，同理可得：
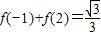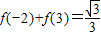，．证明：设x1+x2=1，
=
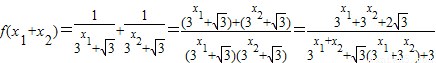
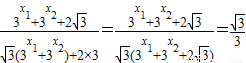
点评：本题主要考查归纳推理，一般思路是从具体到一般，得到一般性结论，然后再证明．属中档题．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|