题目内容

设a＞0，

是R上的偶函数．
(1)求a的值；
(2)证明f(x)在(0，+∞)上是增函数．

（1）解：依题意，对一切x∈R有f(-x)=f(x)成立，即

，
∴

=0，
对一切x∈R成立，由此得到a-

=0，∴a²=1，
又a＞0，∴a=1。
（2）证明：设0＜x₁＜x₂，
则

＜0，
∴f(x₁)＜f(x₂)，
∴f(x)在(0，+∞)上为增函数．

练习册系列答案

仁爱英语同步整合方案系列答案

仁爱英语同步活页AB卷系列答案

仁爱英语同步练习与测试系列答案

仁爱英语同步练习簿系列答案

仁爱英语同步练测考系列答案

仁爱英语同步语法系列答案

仁爱英语同步过关测试卷系列答案

仁爱英语基础训练系列答案

0系列答案

仁爱英语教材讲解系列答案

相关题目

（2011•嘉定区三模）已知k∈R，a＞0且a≠1，b＞0且b≠1，函数f（x）=a^x+k•b^x．
（1）如果实数a、b满足a＞1，ab=1，试判断函数f（x）的奇偶性，并说明理由；
（2）设a＞1＞b＞0，k≤0，判断函数f（x）在R上的单调性并加以证明；
（3）若a=2，b=

，且k＞0，问函数f（x）的图象是不是轴对称图形？如果是，求出函数f（x）图象的对称轴；如果不是，请说明理由．

已知定义在R上的函数f（x）满足：
①对任意的实数x，y，有f（x+y+1）=f（x-y+1）-f（x）f（y）；
②f（1）=2；
③f（x）在[0，1]上为增函数．
（Ⅰ）求f（0）及f（-1）的值；
（Ⅱ）判断函数f（x）的奇偶性，并证明；
（Ⅲ）（说明：请在（ⅰ）、（ⅱ）问中选择一问解答即可．）
（ⅰ）设a，b，c为周长不超过2的三角形三边的长，求证：f（a），f（b），f（c）也是某个三角形三边的长；
（ⅱ）解不等式f（x）＞1．

已知k∈R，a＞0且a≠1，b＞0且b≠1，函数f（x）=a^x+k•b^x．
（1）如果实数a、b满足a＞1，ab=1，试判断函数f（x）的奇偶性，并说明理由；
（2）设a＞1＞b＞0，k≤0，判断函数f（x）在R上的单调性并加以证明；
（3）若a=2， $数学公式$ ，且k＞0，问函数f（x）的图象是不是轴对称图形？如果是，求出函数f（x）图象的对称轴；如果不是，请说明理由．

已知定义在R上的函数f（x）满足：
①对任意的实数x，y，有f（x+y+1）=f（x-y+1）-f（x）f（y）；
②f（1）=2；
③f（x）在[0，1]上为增函数．
（Ⅰ）求f（0）及f（-1）的值；
（Ⅱ）判断函数f（x）的奇偶性，并证明；
（Ⅲ）（说明：请在（ⅰ）、（ⅱ）问中选择一问解答即可．）
（ⅰ）设a，b，c为周长不超过2的三角形三边的长，求证：f（a），f（b），f（c）也是某个三角形三边的长；
（ⅱ）解不等式f（x）＞1．

已知k∈R，a＞0且a≠1，b＞0且b≠1，函数f（x）=a^x+k•b^x．
（1）如果实数a、b满足a＞1，ab=1，试判断函数f（x）的奇偶性，并说明理由；
（2）设a＞1＞b＞0，k≤0，判断函数f（x）在R上的单调性并加以证明；
（3）若a=2，

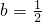，且k＞0，问函数f（x）的图象是不是轴对称图形？如果是，求出函数f（x）图象的对称轴；如果不是，请说明理由．