题目内容

设[x]表示不超过x的最大整数，如：[1.5]=1，[-1.5]=-2．若集合A={x|x²-[x]-1=0}， $数学公式$ ，则A∩B=________．

$\text{[math]}$
分析：把集合A中的方程变形为x²=[x]+1，根据题中的新定义可知x²为整数，然后求出方程x²-x-1=0的解，根据新定义求出解在新定义条件下满足的值，经过检验得到集合A中的元素，由指数函数的单调性可得集合B中不等式的解集即可求出集合A，求出两集合的交集即可．
解答：由集合A中的等式x²-[x]-1=0变形得：x²=[x]+1，由题意可知x²为整数，
而x²-x-1=0的解为x= $\text{[math]}$ ，则[ $\text{[math]}$ ]=1，[ $\text{[math]}$ ]=-1，
所以x²=[x]+1=1+1=2，解得x=± $\text{[math]}$ 或x²=-1+1=0，解得x=0，
经检验：x=- $\text{[math]}$ ，x=0不合题意舍去，所以x= $\text{[math]}$ ，则集合A={ $\text{[math]}$ }；
由集合B中的不等式得：2^-1＜2^x＜2²，由2＞1，得到指数函数为增函数，
所以-1＜x＜2，则集合B=（-1，2），
则A∩B={ $\text{[math]}$ }．
故答案为：{ $\text{[math]}$ }．
点评：此题考查学生掌握新定义的意义以及灵活运用新定义解决数学问题，掌握指数函数的单调性，会求两集合的交集，是一道中档题．

练习册系列答案

三维导学案系列答案

单元双测试卷系列答案

活页练习西安出版社系列答案

作业课课清系列答案

轻松15分达标作业系列答案

节节高解析测评系列答案

海淀金卷系列答案

全能金卷全能卷王系列答案

名师优选全程练考卷系列答案

本真试卷系列答案

相关题目

设[x]表示不超过x的最大整数（如[2]=2，[

]=1），对于给定的n∈N^*，定义

n(n-1)…(n-[x]+1)

x(x-1)…(x-[x]+1)

，x∈[1，+∞），则当x∈[

，3)时，函数

的值域是（　　）

)∪[28，56）

设[x]表示不超过x的最大整数（如：[1]=1，[

]=2），则定义在[2，4）的函数f（x）=x^[x]-ax（其中a为常数，且a≤4）的值域为（　　）

A、[4-2a，64-4a）

B、[4-2a，9-3a）∪[27-3a，64-4a）

C、[9-3a，64-4a）

D、[4-2a，9-3a]∪（27-3a，64-4a]

（2010•台州二模）设[x]表示不超过x的最大整数（如[2]=2，[1.3]=1），已知函数f(x)=

（x≥0），当f（x）＜1时，实数x的取值范围是

设[x]表示不超过x的最大整数（如[2]=2，[

]=1），对于给定的n∈N^*，定义

n(n-1)…(n-[x]+1)

x(x-1)…(x-[x]+1)

，x∈[1，+∞），则当x∈[

，3)时，函数C₈^x的值域是（　　）

)∪[28，56）

设[x]表示不超过x的最大整数，（如[2]=2，

=1），对于给定的n∈N⁺，定义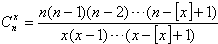

，x∈[1，+∞），则

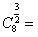（），当x∈[2，3）时，函数

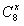的值域是（）。