题目内容
11、设a1，a2，…an是1，2，…，n的一个排列，把排在A的左边且比ai小的数的个数称为ai的顺序数（i=1，2，…n）．如：在排列6，4，5，3，2，1中，5的顺序数为1，2的顺序数为0．则在1至8这八个数字构成的全排列中，同时满足8的顺序数为2，6的顺序数为3，2的顺序数为0的不同排列的种数为（ ）
分析：8一定在第三位，前面有几位数，顺序数就为几，7一定在第五位，因为前面除了8以外所有数都比他小，这两个可以不考虑
，题目变化为数列 123456 保证5的顺序数是3就可以了，再分类求解.6在5前面和6在5后面，根据分类和分步得到结果．
，题目变化为数列 123456 保证5的顺序数是3就可以了，再分类求解.6在5前面和6在5后面，根据分类和分步得到结果．
解答：解：8一定在第三位，前面有几位数，顺序数就为几
而且对其他数的顺序数没有影响，因为8最大
7一定在第五位，因为前面除了8以外所有数都比他小
现在对其他数的顺序数没有影响，因为在8后面又比其他数小
这两个可以不考虑
∴题目变化为数列 123456 保证5的顺序数是3就可以了，
∴分两种情况
.6在5前面，此时5一定在第5位，除6外前面有3个数，故有4×4×3×2×1=96种
6在5后面，此时5一定在第4位上，6在后面两个数字上，故有2×4×3×2×1=48
∴共有96+48=144
故选B
而且对其他数的顺序数没有影响，因为8最大
7一定在第五位，因为前面除了8以外所有数都比他小
现在对其他数的顺序数没有影响，因为在8后面又比其他数小
这两个可以不考虑
∴题目变化为数列 123456 保证5的顺序数是3就可以了，
∴分两种情况
.6在5前面，此时5一定在第5位，除6外前面有3个数，故有4×4×3×2×1=96种
6在5后面，此时5一定在第4位上，6在后面两个数字上，故有2×4×3×2×1=48
∴共有96+48=144
故选B
点评：本题考查分类计数原理，考查分步计数原理，本题是一个综合题目，把分类和分步放在一起用，考查数字的排列问题，是一个典型的排列组合问题．
练习册系列答案
相关题目
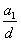的数值；