题目内容
已知函数f(x)=2x-2-x,数列{an}满足f(log2an)=-2n,
(1)求数列{an}的通项公式;
(2)证明数列{an}是递减数列。
(1)求数列{an}的通项公式;
(2)证明数列{an}是递减数列。
(1)解:∵f(x)=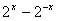 ,f(log2an)=-2n,
,f(log2an)=-2n,
∴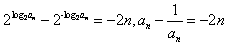 ,
,
∴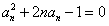 ,解得
,解得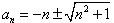 ,
,
∵an>0,
∴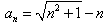 ,n∈N*;
,n∈N*;
(2)证明: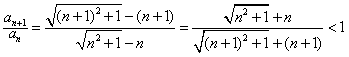 ,
,
∵an>0,
∴an+1<an,
∴数列{an}是递减数列。
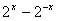 ,f(log2an)=-2n,
,f(log2an)=-2n,∴
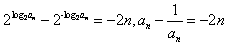 ,
,∴
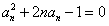 ,解得
,解得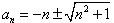 ,
,∵an>0,
∴
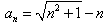 ,n∈N*;
,n∈N*;(2)证明:
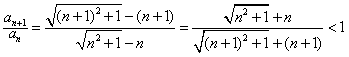 ,
,∵an>0,
∴an+1<an,
∴数列{an}是递减数列。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目