题目内容
(理)已知函数f(x)=
,x∈(0,+∞),数列{an}满足a1=1,an+1=f(an);数列{bn}满足b1=
,bn+1=
,其中Sn为数列{bn}的前n项和,n=1,2,3,….(1)求数列{an}和数列{bn}的通项公式;
(2)设Tn=
,证明Tn＜5.
答案：(理)(1)解：∵f(x)=,an+1=f(an),∴an+1=.∴+2.
∴为以
=1为首项、以2为公差的等差数列.∴
=1+(n-1)·2.∴an=
.
又∵f(x)=
,bn+1=
,∴bn+1=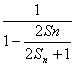
=2Sn+1.∴bn+2=2Sn+1+1.
∴bn+2-bn+1=2(Sn+1-Sn).∴bn+2=3bn+1.∵b1=
,b2=2S1+1=2,
∴{bn}从第二项起成等比数列,公比为3.bn=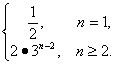
.
(2)证明:依题意
Tn=2+
［3·1+5·
+7·(
)2+…+(2n-1)(
)n-2］,
令An=3·1+5·
+7·(
)2+…+(2n-1)·(
)n-2,
An=3·
+5·(
)2+7·(
)3+…+(2n-3)·(
)n-2+(2n-1)·(
)n-1,
∴
An=3·1+2［
+(
)2+(
)3+…+(
)n-2］-(2n-1)·(
)n-1
=3+2·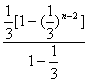
-(2n-1)(
)n-1.∴An=6-
(
)n-2-
·(2n-1)(
)n-1.
∴Tn=5-
·(
)n-2-
·(2n-1)(
)n-1＜5.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（理）已知函数
（2011•普陀区三模）（理）已知函数