题目内容
12.给出下列命题:①直线y=0与曲线y=x3相切;
②若f′(x0)=0,则x0是f(x)的极值点;
③若f(x)可导且减于(a,b),则f′(x)<0恒成立于(a,b);
④对任意a≠0,[ln(ax)]′=$\frac{1}{x}$
其中正确命题的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 对四个命题分别进行判断,即可得出结论.
解答 解:①直线y=0与曲线y=x3相切,正确;
②若f′(x0)=0,则连续函数y=f(x)在点x0处不一定取极值,例如:f(x)=x3,故不正确;
③若f(x)可导且减于(a,b),则f′(x)<0恒成立于(a,b),正确;
④对任意a≠0,[ln(ax)]′=$\frac{a}{x}$故不正确
故选:C.
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
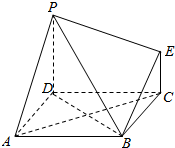 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且