题目内容
设P1(4,-3),P2(-2,6),且P在P1P2的延长线上,使|
|=2|
|,则点P的坐标 ( )
| P1P |
| PP2 |
| A.(-8,15) | B.(0,3) | C.(-
| D.(1,
|
解法一:设分点P(x,y),由题意知
=-2
,P分有向线段P1P2成的 比 λ=-2,
根据向量相等的条件得:(x-4,y+3)=-2(-2-x,6-y),
x-4=2x+4,y+3=2y-12,∴x=-8,y=15,
∴P(-8,15).
解法二:设分点P(x,y),∵
=-2
,P分有向线段P1P2成的 比 λ=-2,
代入定比分点坐标公式得:
∴x=
=-8,
y=
=15,
∴P(-8,15)
故选A.
| P1P |
| PP2 |
根据向量相等的条件得:(x-4,y+3)=-2(-2-x,6-y),
x-4=2x+4,y+3=2y-12,∴x=-8,y=15,
∴P(-8,15).
解法二:设分点P(x,y),∵
| P1P |
| PP2 |
代入定比分点坐标公式得:
∴x=
| 4-2(-2) |
| 1-2 |
y=
| -3-2×6 |
| 1-2 |
∴P(-8,15)
故选A.

练习册系列答案
相关题目
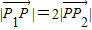 ,则点P的坐标 ( )
,则点P的坐标 ( ) ,
,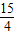 )
) )
)