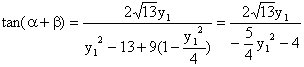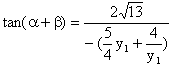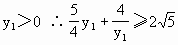题目内容
已知P是椭圆 =1(a>b>0)上一点,
=1(a>b>0)上一点, 是椭圆的焦点,
是椭圆的焦点, ,且点P到两准线的距离分别为
,且点P到两准线的距离分别为

(Ⅰ)求椭圆的准线方程;
(Ⅱ)求椭圆的方程;
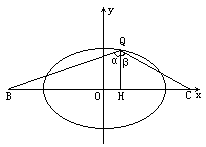
(Ⅲ)又若已知定点B( )、C(
)、C( ),Q(
),Q( )是椭圆上一动点(
)是椭圆上一动点( >0),QH⊥x轴,垂足为H,∠BQH=α,∠HQC=β.
>0),QH⊥x轴,垂足为H,∠BQH=α,∠HQC=β.
求tan(α+β)的最小值,并求此时Q点的坐标.
答案:
解析:
解析:
|
解:(Ⅰ)∵椭圆上点P到两准线的距离分别为 ∴ ∴ ∴椭圆的准线方程为x=± (Ⅱ)法一:如图,由
设椭圆离心率为e,由椭圆的第二定义及勾股定理得: ∴ ∴ ∴椭圆的方程为 法二:设P( 由① 由⑤ 由④ 由②得 ∴ ⑥、⑦、⑧、⑨代入③,得 化简,整理得: ∴c= 代入⑥得 ∴椭圆的方程为 (Ⅲ)∵点Q的坐标为(
∴ ∴ 即 又Q ∴ ∴ ∴ ∵ ∴ 当且仅当 此时 ∴ |

练习册系列答案
相关题目
 ,
,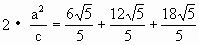 ,
,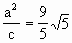 ,
,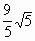 .
.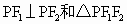 是直角三角形.
是直角三角形.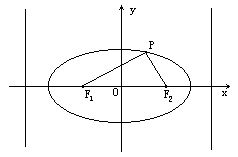
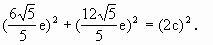
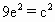 .
.
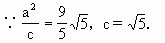
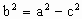 =4.
=4.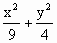 =1.
=1.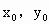 )由对称性,不妨设
)由对称性,不妨设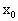 >0,由题意,得
>0,由题意,得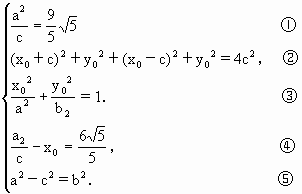


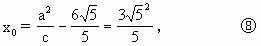
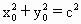 ,
,
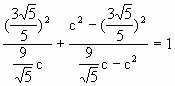
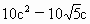 =0,
=0,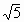 .
. =9,代入⑦得
=9,代入⑦得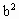 =4,
=4,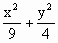 =1.
=1. ),
),
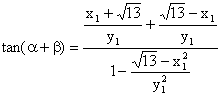
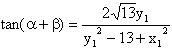
 上的动点,
上的动点,