题目内容
如图所示,S是边长为a的正△ABC所在平面外一点,SA=SB=SC=a,E、F分别是SC和AB的中点.
(1)求异面直线SC和AB的距离;
(2)求异面直线SA和EF所成的角.
解析:(1)连结SF、CF,?
∵△SAB、△CAB是正三角形,∴SF=CF=![]() a,且SF虯B,CF⊥AB.?
a,且SF虯B,CF⊥AB.?
又SF∩CF=F,∴AB⊥面SFC.?
∴AB⊥EF于F.?
又SF=CF,∴△FSC是等腰三角形.?
又E是SC中点,∴FE⊥SC于E.?
∴EF是SC与AB的公垂线段.?
在Rt△SEF中,SF=![]() a,SE=
a,SE=![]() a,?
a,?
∴由勾股定理可知EF=![]() .?
.?
因此,异面直线SC与AB的距离为![]() .?
.?
(2)取AC中点M,连结EM、FM.?
∵E、F、M分别为SC、AB、CA中点,?
∴EM∥SA,FM∥CB,?
且EM=![]() SA,FM=
SA,FM=![]() CB.?
CB.?
∴EM=FM=12a.?
∴∠MEF是SA与EF所成的角或其补角.?
∵EM=FM=![]() a,EF=
a,EF=![]() a,?
a,?
∴EF2=FM2+EM2,即FM⊥EM.?
∴△EMF是等腰直角三角形.?
∴∠MFE=45°,即SA与EF所成的角是45°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
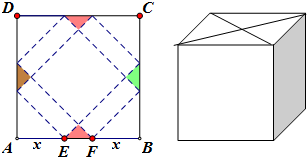 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
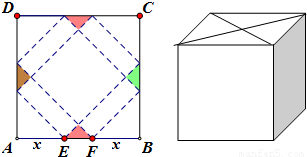 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).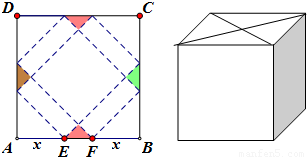 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).