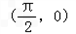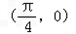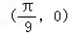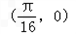题目内容
将函数 的图象上各点的横坐标伸长到原来的2倍,再向左平移
的图象上各点的横坐标伸长到原来的2倍,再向左平移 个单位,所得函数图象的一个对称中心是
个单位,所得函数图象的一个对称中心是
- A.
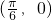
- B.

- C.
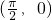
- D.
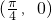
A
分析:根据y=Asin(ωx+∅)的图象变换规律可得所得图象对应的函数为y=sin(2x+ ),由2x+
),由2x+ =kπ,k∈z,可得对称中心的横坐标,从而得出结论.
=kπ,k∈z,可得对称中心的横坐标,从而得出结论.
解答:将函数 的图象上各点的横坐标伸长到原来的2倍,可得函数y=sin(2x+
的图象上各点的横坐标伸长到原来的2倍,可得函数y=sin(2x+ )的图象,
)的图象,
再向左平移 个单位,可得函数y=sin[2(x+
个单位,可得函数y=sin[2(x+ )+
)+ ]=sin(2x+
]=sin(2x+ )的图象,
)的图象,
由2x+ =kπ,k∈z,可得 x=
=kπ,k∈z,可得 x= -
- ,故所得函数图象的对称中心为(
,故所得函数图象的对称中心为(  -
- ,0),k∈z.
,0),k∈z.
令 k=1 可得一个对称中心为( ,0),
,0),
故选A.
点评:本题主要考查y=Asin(ωx+∅)的图象变换规律,正弦函数的对称中心,属于中档题.
分析:根据y=Asin(ωx+∅)的图象变换规律可得所得图象对应的函数为y=sin(2x+
 ),由2x+
),由2x+ =kπ,k∈z,可得对称中心的横坐标,从而得出结论.
=kπ,k∈z,可得对称中心的横坐标,从而得出结论.解答:将函数
 的图象上各点的横坐标伸长到原来的2倍,可得函数y=sin(2x+
的图象上各点的横坐标伸长到原来的2倍,可得函数y=sin(2x+ )的图象,
)的图象,再向左平移
 个单位,可得函数y=sin[2(x+
个单位,可得函数y=sin[2(x+ )+
)+ ]=sin(2x+
]=sin(2x+ )的图象,
)的图象,由2x+
 =kπ,k∈z,可得 x=
=kπ,k∈z,可得 x= -
- ,故所得函数图象的对称中心为(
,故所得函数图象的对称中心为(  -
- ,0),k∈z.
,0),k∈z.令 k=1 可得一个对称中心为(
 ,0),
,0),故选A.
点评:本题主要考查y=Asin(ωx+∅)的图象变换规律,正弦函数的对称中心,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 的图象上各点的横坐标长到原来的3倍,纵坐标不变,再把所得函数图象向右平行移动
的图象上各点的横坐标长到原来的3倍,纵坐标不变,再把所得函数图象向右平行移动 个单位长度,得到的函数图象的一个对称中心是
个单位长度,得到的函数图象的一个对称中心是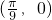
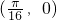
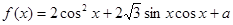 ,且当
,且当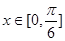 时,
时,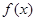 的最小值为2.
的最小值为2.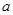 的值,并求
的值,并求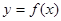 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的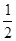 倍,再把所得图象向右平移
倍,再把所得图象向右平移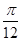 个单位,得到函数
个单位,得到函数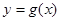 ,求方程
,求方程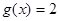 在区间
在区间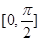 上的所有根之和.
上的所有根之和.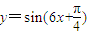 的图象上各点的横坐标伸长到原来的3倍,再向右平移
的图象上各点的横坐标伸长到原来的3倍,再向右平移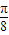 个单位,得到的函数的一个对称中心( )
个单位,得到的函数的一个对称中心( )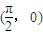
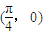
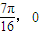 )
)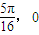 )
)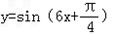 的图象上各点的横坐标长到原来的3倍,纵坐标不变,再把所得函数图象向右平行移动
的图象上各点的横坐标长到原来的3倍,纵坐标不变,再把所得函数图象向右平行移动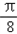 个单位长度,得到的函数图象的一个对称中心是
个单位长度,得到的函数图象的一个对称中心是