Question

设函数y=f（x），满足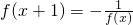，对一切x∈R都成立，又知当（1，3]时，f（x）=2^-x，则f（2013）=________．

Answer 1

分析：根据已知等式利用变量代换，可得f（x+2）=f（x），因此f（x）是周期为2的函数，由此可得f（2013）=f（3），结合当（1，3]时，f（x）=2^-x，可得f（2013）的值．
解答：∵满足，
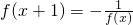∴以x+1代替x，得=-=f（x）
因此，函数f（x）是周期为2的函数
∴f（2013）=f（3+2010）=f（3+1005×2）=f（3）=2^-3=
故答案为：
点评：本题给出抽象函数的部分性质，求f（2013）的值，着重考查了函数的周期性和函数值的求法等知识，属于基础题．