题目内容
某班共有26名同学参加了学校组织的数学、英语两科竞赛,其中两科都取得优秀的有8人,数学取得优秀但英语未取得优秀的有12人,英语取得优秀而数学未取得优秀的有4人,画出Venn图并分别求出数学取得优秀的人数、英语取得优秀的人数及两科均未取得优秀的人数。
解:如图,设全集U={某班26名学生},集合A={数学取得优秀的同学},集合B={英语取得优秀的同学}
设集合A中的元素个数表示为card(A),则card(U)=26,card(A∩B)=8,card(A∩CUB)=12,card(B∩ CUA) =4,由Venn图可知,数学取得优秀的人数为20人,英语取得优秀的人数为12人,两科均未取得优秀的人数为26-(12+8+4)=2 (人)。

设集合A中的元素个数表示为card(A),则card(U)=26,card(A∩B)=8,card(A∩CUB)=12,card(B∩ CUA) =4,由Venn图可知,数学取得优秀的人数为20人,英语取得优秀的人数为12人,两科均未取得优秀的人数为26-(12+8+4)=2 (人)。


练习册系列答案
相关题目
为加强中学生实践、创新能力和同队精神的培养,促进教育教学改革,郑州市教育局举办了全市中学生创新知识竞赛.某校举行选拔赛,共有200名学生参加,为了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
(I )若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,199,试写出第二组第一位学生的编号;
(II)求出a,b,c,d,e的值(直接写出结果),并作出频率分布直方图;
(III)若成绩在95.5分以上的学生为一等奖,现在,从所有一等奖同学中随机抽取5名同学代表学校参加决赛,某班共有3名同学荣获一等奖,若该班同学参加决赛人数记为X,求X的分布列和数学期望.
| 分组 | 频数 | 频率 | |
| 一 | 60.5~70.5 | A | 0.26 |
| 二 | 70.5~80.5 | 15 | C |
| 三 | 80.5~90.5 | 18 | 0.36 |
| 四 | 90.5~100.5 | B | D |
| 合计 | 50 | E | |
(II)求出a,b,c,d,e的值(直接写出结果),并作出频率分布直方图;
(III)若成绩在95.5分以上的学生为一等奖,现在,从所有一等奖同学中随机抽取5名同学代表学校参加决赛,某班共有3名同学荣获一等奖,若该班同学参加决赛人数记为X,求X的分布列和数学期望.
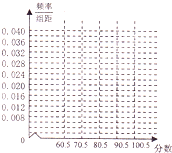 为了加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取了50名学生的成绩进行统计.请你根据尚未完成的频率分布表,解答下列问题:
为了加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取了50名学生的成绩进行统计.请你根据尚未完成的频率分布表,解答下列问题: