题目内容
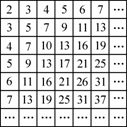
下表中数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为
aij(ij∈N+),则:
(Ⅰ)a99=
(Ⅱ)表中数82共出现
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 3 | 5 | 7 | 9 | 11 | 13 | … |
| 4 | 7 | 10 | 13 | 16 | 19 | … |
| 5 | 9 | 13 | 17 | 21 | 25 | … |
| 6 | 11 | 16 | 21 | 26 | 31 | … |
| 7 | 13 | 19 | 25 | 31 | 37 | … |
| … | … | … | … | … | … | … |
(Ⅰ)a99=
82
82
;(Ⅱ)表中数82共出现
5
5
次.分析:(I)根据表中的规律可得第i行等差数列的公差为i,由此算出第一行数组成的数列通项为a1j=j+1,再根据第j列等差数列的公差等于j,算出aij=ij+1.由此代入数据即可算出a99的值;
(II)由(I)中求出的通项公式aij=ij+1,可得aij=82即ij=81,算出i、j的情况有5种,由此可得表中数82共出现5次.
(II)由(I)中求出的通项公式aij=ij+1,可得aij=82即ij=81,算出i、j的情况有5种,由此可得表中数82共出现5次.
解答:解:根据题意,第i行的等差数列的公差为i,第j列的等差数列的公差等于j,(i、j∈N+),
∴第一行数组成的数列a1j(j=1,2,…)是以2为首项,公差为1的等差数列,
可得a1j=2+(j-1)×1=j+1,
又∵第j列数组成的数列A1j(i=1,2,…)是以a1j为首项,公差为j的等差数列,
∴aij=a1j+(i-1)×j=(j+1)+(i-1)×j=ij+1.
(I)∵aij=ij+1,∴a99=9×9+1=82;
(II)由aij=ij+1=82,得ij=81,
∴i=81且j=1、i=1且j=81、i=3且j=27、i=27且j=3或i=j=9,可得等于82的项共有5项.
因此表中82总共出现5次.
故答案为:82,5
∴第一行数组成的数列a1j(j=1,2,…)是以2为首项,公差为1的等差数列,
可得a1j=2+(j-1)×1=j+1,
又∵第j列数组成的数列A1j(i=1,2,…)是以a1j为首项,公差为j的等差数列,
∴aij=a1j+(i-1)×j=(j+1)+(i-1)×j=ij+1.
(I)∵aij=ij+1,∴a99=9×9+1=82;
(II)由aij=ij+1=82,得ij=81,
∴i=81且j=1、i=1且j=81、i=3且j=27、i=27且j=3或i=j=9,可得等于82的项共有5项.
因此表中82总共出现5次.
故答案为:82,5
点评:本题给出“森德拉姆素数筛”的例子,求表格中的指定项,并求82在表中出现了几次.着重考查了等差数列的通项公式及其应用的知识,属于中档题.

练习册系列答案
相关题目

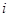 行第
行第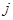 列的数为
列的数为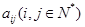 ,则:
,则:
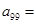 ; (Ⅱ)表中数
; (Ⅱ)表中数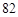 共出现 次.
共出现 次.