已知正四棱锥底面边为2cm.高为$\sqrt{3}$cm.则它的侧面积为8cm3．题目和参考答案——青夏教育精英家教网—

题目内容

14．已知正四棱锥底面边为2cm，高为$\sqrt{3}$cm，则它的侧面积为8cm³．

分析作出棱锥的高和斜高，利用勾股定理计算斜高从而得出侧面积．

解答解：作出正四棱锥的高EO，垂足为O，则OE=$\sqrt{3}$，O为正方形ABCD的中心，
取CD的中点M，连结EM，OM，则OM=$\frac{1}{2}$BC=1，
∴EM=$\sqrt{E{O}^{2}+O{M}^{2}}$=2，
∴S_侧面积=4S_△ECD=4×$\frac{1}{2}×2×2$=8．
故答案为：8．

点评本题考查了棱锥的结构特征，表面积计算，属于基础题．

练习册系列答案

5．已知圆C：x²+y²-6x-4y+4=0，点P（6，0）．
（1）求过点P且与圆C相切的直线方程l；
（2）若圆M与圆C外切，且与x轴切于点P，求圆M的方程．

2．下列各组函数中，表示同一个函数的是（　　）

	A．	f（x）=$\sqrt{{x}^{2}}$，g（x）=\|x\|		B．	f（x）=x⁰，g（x）=1
	C．	f（x）=$\frac{{x}^{2}-1}{x+1}$，g（x）=x-1		D．	f（x）=$\sqrt{x+1}$•$\sqrt{x-1}$，g（x）=$\sqrt{{x}^{2}-1}$

9．已知向量$\overrightarrow{a}$=（$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$），$\overrightarrow{b}$=（1，$\sqrt{3}$），$\overrightarrow{x}$=$\overrightarrow{a}$+（t²-3）$\overrightarrow{b}$，$\overrightarrow{y}$=-k$\overrightarrow{a}$+t$\overrightarrow{b}$，若$\overrightarrow{x}$与$\overrightarrow{y}$垂直，则k可用t的表达式表示为k=4t（t²-3）．

19．若复数z满足|z|=2，则|1+$\sqrt{3}$i+z|的取值范围是（　　）

6．已知动圆Q过定点F（0，-1），且与直线l：y=1相切，椭圆N的对称轴为坐标轴，O点为坐标原点，F是其一个焦点，又点A（0，2）在椭圆N上．
（Ⅰ）求动圆圆心Q的轨迹M的标准方程和椭圆N的标准方程；
（Ⅱ）若过F的动直线m交椭圆N于B，C点，交轨迹M于D，E两点，设S₁为△ABC的面积，S₂为△ODE的面积，令Z=S₁S₂，试求Z的取值范围．

3．叙述并用坐标法证明余弦定理．

4．

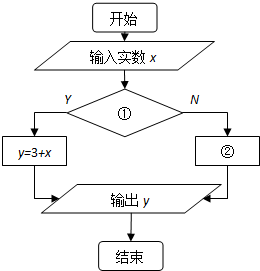已知函数y=|x+3|，向量程序框表示的是给出x值，求所对应的函数值的算法，请将该程序框图补充完整，其中①处应填x≥-3；②处应填y=-x-3．

试题分类