题目内容
已知数列{an}满足a1=1,an=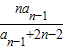 (n≥2).
(n≥2).(1)求a2,a3,
(2)求数列{an}的通项公式;
(3)设{an}的前n项和Sn,证明:Sn>2-
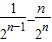 .
.
【答案】分析:(1)a1=1,再an=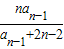 (n≥2)中令n=2求a2,令n=3求a3.
(n≥2)中令n=2求a2,令n=3求a3.
(2)由an=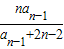 (n≥2),两边取倒数,得出
(n≥2),两边取倒数,得出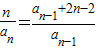 =
=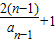 ,令cn=
,令cn=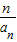 ,构造得出数列{cn+1}是以2为首项,2为公比的等比数列,
,构造得出数列{cn+1}是以2为首项,2为公比的等比数列,
通过数列{cn+1}的通项公式求an.
(3)由(2)an=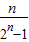 ,直接求Sn不易求.将每项进行缩小,an=
,直接求Sn不易求.将每项进行缩小,an=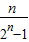 >
>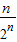 ,利用错位相消法将右边相加、化简后,即可证明.
,利用错位相消法将右边相加、化简后,即可证明.
解答:解:(1)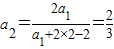 ,
,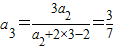
(2)an=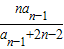 (n≥2).
(n≥2).
∴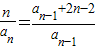 =
=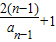 ,
,
令cn=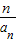 ,则cn=2cn-1+1,cn+1=2(cn-1+1),
,则cn=2cn-1+1,cn+1=2(cn-1+1),
又c1+1=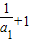 =2,所以数列{cn+1}是以2为首项,2为公比的等比数列,
=2,所以数列{cn+1}是以2为首项,2为公比的等比数列,
所以cn+1=2n,cn=2n-1,
∴an=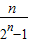
(3)an=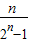 >
>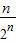 ,所以Sn>a1+a2+…+an=
,所以Sn>a1+a2+…+an=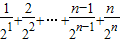
令Tn=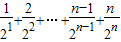 ①
①
则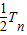 =
=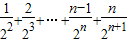 ②
②
①-②得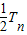 =
=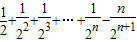 =
=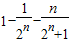
Tn=2-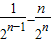 .
.
所以Sn>2-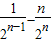 .
.
点评:本题是中档题,考查数列的递推关系式的应用,数列通项公式求解,数列求和,放缩法不等式的证明,考查计算能力,转化思想.
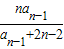 (n≥2)中令n=2求a2,令n=3求a3.
(n≥2)中令n=2求a2,令n=3求a3.(2)由an=
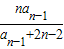 (n≥2),两边取倒数,得出
(n≥2),两边取倒数,得出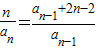 =
=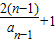 ,令cn=
,令cn=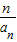 ,构造得出数列{cn+1}是以2为首项,2为公比的等比数列,
,构造得出数列{cn+1}是以2为首项,2为公比的等比数列,通过数列{cn+1}的通项公式求an.
(3)由(2)an=
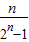 ,直接求Sn不易求.将每项进行缩小,an=
,直接求Sn不易求.将每项进行缩小,an=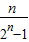 >
>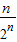 ,利用错位相消法将右边相加、化简后,即可证明.
,利用错位相消法将右边相加、化简后,即可证明.解答:解:(1)
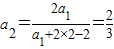 ,
,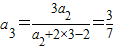
(2)an=
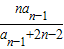 (n≥2).
(n≥2).∴
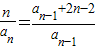 =
=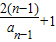 ,
,令cn=
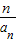 ,则cn=2cn-1+1,cn+1=2(cn-1+1),
,则cn=2cn-1+1,cn+1=2(cn-1+1),又c1+1=
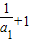 =2,所以数列{cn+1}是以2为首项,2为公比的等比数列,
=2,所以数列{cn+1}是以2为首项,2为公比的等比数列,所以cn+1=2n,cn=2n-1,
∴an=
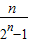
(3)an=
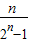 >
>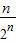 ,所以Sn>a1+a2+…+an=
,所以Sn>a1+a2+…+an=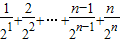
令Tn=
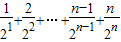 ①
①则
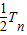 =
=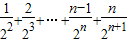 ②
②①-②得
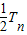 =
=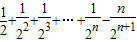 =
=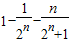
Tn=2-
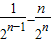 .
.所以Sn>2-
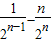 .
.点评:本题是中档题,考查数列的递推关系式的应用,数列通项公式求解,数列求和,放缩法不等式的证明,考查计算能力,转化思想.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目