题目内容
设函数f(x)=sinx-cosx+x+1，0＜x＜2π，求函数f(x)的单调区间与极值。
解：由f(x)=sinx-cosx+x+1，0＜x＜2π，知f′(x)=cosx+sinx+1，
于是，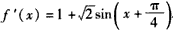
，
令f′(x)=0，从而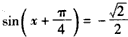
，得x=π或
，
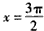当x变化时，f′(x)，f(x)变化情况如下表：
因此，由上表知f（x）的单调增区间为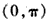
与
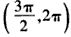，单调减区间为
，
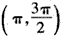极小值为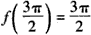
，极大值为f(π)=π+2．
于是，
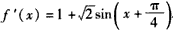，令f′(x)=0，从而
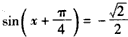，得x=π或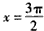，当x变化时，f′(x)，f(x)变化情况如下表：
因此，由上表知f（x）的单调增区间为
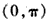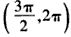与，单调减区间为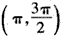，极小值为
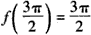，极大值为f(π)=π+2． 
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目