题目内容
已知f(x)=| x+2 |
| x+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 10 |
分析：将x、
代入函数解析式，然后相加即可得到f（x）+f（
）=3，再求出f（1），即可求出f(1)+f(2)+…+f(10)+f(
)+f(
)+…f(
)的值．
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 10 |
解答：解：∵f(x)=
，∴f（x）+f（
）=1+
+1+
=3
∴f（2）+f（
）=3，f（3）+f（
）=3，…
而f（1）=
∴f(1)+f(2)+…+f(10)+f(
)+f(
)+…f(
)=28.5
故答案为：28.5
| x+2 |
| x+1 |
| 1 |
| x |
| 1 |
| x+1 |
| 1 | ||
|
∴f（2）+f（
| 1 |
| 2 |
| 1 |
| 3 |
而f（1）=
| 3 |
| 2 |
∴f(1)+f(2)+…+f(10)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 10 |
故答案为：28.5
点评：本题主要考查已知函数解析式求函数值的问题，一般用代入法，同时考查了计算能力，属于基础题．
练习册系列答案
相关题目
已知f(x)=sin(x+
)，g(x)=cos(x-
)，则下列结论中正确的是（ ）
| π |
| 2 |
| π |
| 2 |
| A、函数y=f（x）•g（x）的最大值为1 | ||||
B、函数y=f（x）•g（x）的对称中心是(
| ||||
C、当x∈[-
| ||||
D、将f（x）的图象向右平移
|
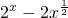，又a是函数g （x）=
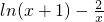的正零点，则f（-2），f（a），f（1.5）的大上关系是