题目内容
设函数f(x)=lnx﹣ ax2﹣bx.
ax2﹣bx.
(1)当a=b= 时,求f(x)的最大值;
时,求f(x)的最大值;
(2)令F(x)=f(x)+ ax2+bx+
ax2+bx+ (0<x≤3),以其图象上任意一点P(x0,y0)为切点的切线的斜率k≤
(0<x≤3),以其图象上任意一点P(x0,y0)为切点的切线的斜率k≤ 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)当a=0,b=﹣1时,方程2mf(x)=x2有唯一实数解,求正数m的值.
 ax2﹣bx.
ax2﹣bx.(1)当a=b=
 时,求f(x)的最大值;
时,求f(x)的最大值;(2)令F(x)=f(x)+
 ax2+bx+
ax2+bx+ (0<x≤3),以其图象上任意一点P(x0,y0)为切点的切线的斜率k≤
(0<x≤3),以其图象上任意一点P(x0,y0)为切点的切线的斜率k≤ 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)当a=0,b=﹣1时,方程2mf(x)=x2有唯一实数解,求正数m的值.
解:(1)依题意,知f(x)的定义域为(0,+∞)
当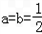 时,
时,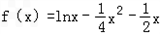 ,
,
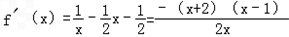 .
.
令f''(x)=0,解得x=1.
当0<x<1时,f''(x)>0,此时f(x)单调递增;
当x>1时,f''(x)<0,此时f(x)单调递减.
所以f(x)的极大值为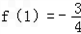 ,此即为最大值.
,此即为最大值.
(2)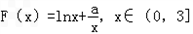 ,
,
所以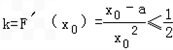 ,,在x0∈(0,3]上恒成立,
,,在x0∈(0,3]上恒成立,
所以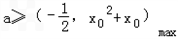 ,x0∈(0,3]
,x0∈(0,3]
当x0=1时,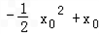 取得最大值
取得最大值 .
.
所以a= .
.
(3)因为方程2mf(x)=x2有唯一实数解,
所以x2﹣2mlnx﹣2mx=0有唯一实数解.
设g(x)=x2﹣2mlnx﹣2mx,
则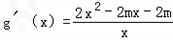 .
.
令g'(x)=0,得x2﹣mx﹣m.
因为m>0,x>0,所以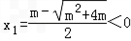 (舍去),
(舍去),
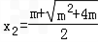 ,
,
当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)单调递减,
当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)单调递增.
当x=x2时,g’(x2)=0 ,g(x2)取最小值g(x2).
因为g(x)=0有唯一解,所以g(x2)=0.
则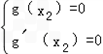 ,即
,即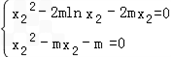
所以2mlnx2+mx2﹣m=0,
因为m>0,所以2lnx2+x2﹣1=0.
设函数h(x)=2lnx+x﹣1,
因为当x>0时,h(x)是增函数,
所以h(x)=0至多有一解.
因为h(I)=0,所以方程的解为(X2)=1,
即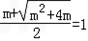 ,
,
解得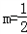
当
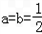 时,
时,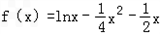 ,
,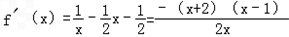 .
.令f''(x)=0,解得x=1.
当0<x<1时,f''(x)>0,此时f(x)单调递增;
当x>1时,f''(x)<0,此时f(x)单调递减.
所以f(x)的极大值为
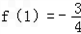 ,此即为最大值.
,此即为最大值.(2)
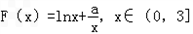 ,
,所以
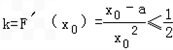 ,,在x0∈(0,3]上恒成立,
,,在x0∈(0,3]上恒成立,所以
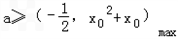 ,x0∈(0,3]
,x0∈(0,3]当x0=1时,
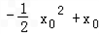 取得最大值
取得最大值 .
.所以a=
 .
.(3)因为方程2mf(x)=x2有唯一实数解,
所以x2﹣2mlnx﹣2mx=0有唯一实数解.
设g(x)=x2﹣2mlnx﹣2mx,
则
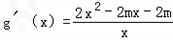 .
.令g'(x)=0,得x2﹣mx﹣m.
因为m>0,x>0,所以
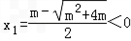 (舍去),
(舍去),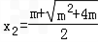 ,
,当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)单调递减,
当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)单调递增.
当x=x2时,g’(x2)=0 ,g(x2)取最小值g(x2).
因为g(x)=0有唯一解,所以g(x2)=0.
则
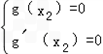 ,即
,即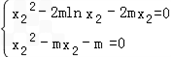
所以2mlnx2+mx2﹣m=0,
因为m>0,所以2lnx2+x2﹣1=0.
设函数h(x)=2lnx+x﹣1,
因为当x>0时,h(x)是增函数,
所以h(x)=0至多有一解.
因为h(I)=0,所以方程的解为(X2)=1,
即
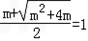 ,
,解得
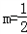

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目