题目内容
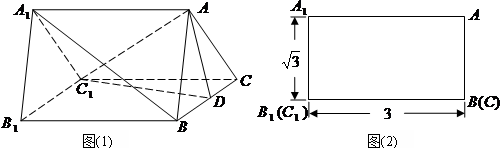
如图(1)是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的正(主)视图如图(2).
(1)求正三棱柱ABC-A1B1C1的体积;
(2)证明:A1B∥平面ADC1;
(3)图(1)中垂直于平面BCC1B1的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)

(1)求正三棱柱ABC-A1B1C1的体积;
(2)证明:A1B∥平面ADC1;
(3)图(1)中垂直于平面BCC1B1的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)

证明:(1)依题意,在正三棱柱中,AD=
,
AA1=3,从而AB=2,AA1⊥平面ABC,
所以正三棱柱的体积V=Sh=
×AB×AD×AA1=
×2×
×3=3
.
(2)连接A1C,设A1C∩AC1=E,
连接DE,因为AA1C1C是正三棱柱的侧面,
所以AA1C1C是矩形,E是A1C的中点,
所以DE是△A1BC的中位线,DE∥A1B,
因为DE?平面ADC1,A1B?平面ADC1,
所以A1B∥平面ADC1.
(3)AD垂直平面BCC1B1,AD?平面ABC、平面ABC∥平面A1B1C1、AD?平面AC1D
所以垂直于平面BCC1B1的平面有:平面ABC、平面A1B1C1、平面AC1D.
| 3 |
AA1=3,从而AB=2,AA1⊥平面ABC,
所以正三棱柱的体积V=Sh=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)连接A1C,设A1C∩AC1=E,
连接DE,因为AA1C1C是正三棱柱的侧面,
所以AA1C1C是矩形,E是A1C的中点,
所以DE是△A1BC的中位线,DE∥A1B,
因为DE?平面ADC1,A1B?平面ADC1,
所以A1B∥平面ADC1.
(3)AD垂直平面BCC1B1,AD?平面ABC、平面ABC∥平面A1B1C1、AD?平面AC1D
所以垂直于平面BCC1B1的平面有:平面ABC、平面A1B1C1、平面AC1D.

练习册系列答案
相关题目
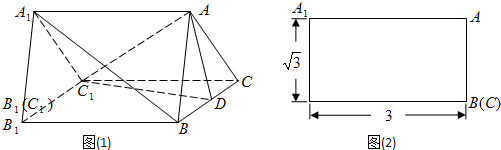
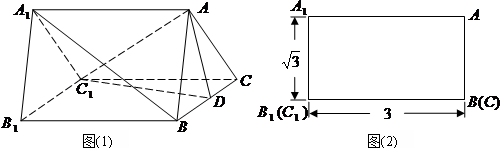
 如图(1)是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的正(主)视图如图(2)
如图(1)是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的正(主)视图如图(2)