题目内容
若
-
=1,点P(x,y)到点(-3,0)的距离为3
,则点P到点(3,0)的距离为 .
| x2 |
| 2 |
| y2 |
| 7 |
| 2 |
分析:由双曲线的方程
-
=1,算出(-3,0)和(3,0)恰好是双曲线的左右焦点,由此利用双曲线的定义加以计算,可得点P到点(3,0)的距离.
| x2 |
| 2 |
| y2 |
| 7 |
解答:解:∵双曲线
-
=1中,a2=2、b2=7,得a=
、b=
,
∴c2=a2+b2=9,得c=3.
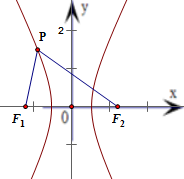
可得双曲线的焦点坐标为F1(-3,0)和F2(3,0).
∵点P(x,y)到左焦点F1(-3,0)的距离为3
,
∴根据双曲线的定义可得:点P到右焦点F2(3,0)的距离d=3
±2a,
即d=5
或
.
∵当d=
时,|PF1|+|PF2|=4
<|F1F2|=6,矛盾
∴d=
不符合题意,舍去.
因此d=5
,即点P到点(3,0)的距离为5
.
故答案为:5
| x2 |
| 2 |
| y2 |
| 7 |
| 2 |
| 7 |

∴c2=a2+b2=9,得c=3.
可得双曲线的焦点坐标为F1(-3,0)和F2(3,0).
∵点P(x,y)到左焦点F1(-3,0)的距离为3
| 2 |
∴根据双曲线的定义可得:点P到右焦点F2(3,0)的距离d=3
| 2 |
即d=5
| 2 |
| 2 |
∵当d=
| 2 |
| 2 |
∴d=
| 2 |
因此d=5
| 2 |
| 2 |
故答案为:5
| 2 |
点评:本题给出双曲线上的点到一个焦点的距离,求它到另一个焦点的距离.着重考查了双曲线的定义与标准方程的知识,属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目