题目内容
已知平行六面体ABCD-A1B1C1D1中，以顶点A为端点的三条棱长都等于1，且两两夹角都为60°，则对角线AC1的长是分析：设
=
，
=
，
=
，则两两夹角为60°，且模均为1．根据向量加法的平行四边形法则，我们易得
=
+
+
=
+
+
．我们易根据向量数量积的运算法则，求出AC1的模，即AC1的长；
| AB |
| a |
| AD |
| b |
| AA 1 |
| C |
| AC 1 |
| AB |
| AD |
| AA 1 |
| a |
| b |
| c |
解答：解：设
=
，
=
，
=
，则两两夹角为60°，且模均为1．
=
+
+
=
+
+
∴|
|2=（
+
+
）2
=3+6×1×1×12=6，
∴|AC1|=6，即AC1的长为
．
故答案为：
．
| AB |
| a |
| AD |
| b |
| AA 1 |
| C |
| AC 1 |
| AB |
| AD |
| AA 1 |
| a |
| b |
| c |
∴|
| AC 1 |
| a |
| b |
| c |
=3+6×1×1×12=6，
∴|AC1|=6，即AC1的长为
| 6 |
故答案为：
| 6 |
点评：本题考查的知识点是空间两点之间的距离运算，根据已知条件，构造向量，将空间两点之间的距离转化为向量模的运算，是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
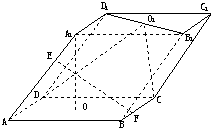如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
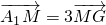，设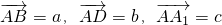
，用向量a、b、c表示向量
；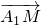