题目内容
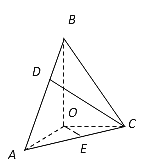
【题目】在三棱锥
中，BO、AO、CO所在直线两两垂直，且AO=CO，∠BAO=60°，E是AC的中点，三棱锥的体积为
(1)求三棱锥的高；
(2)在线段AB上取一点D，当D在什么位置时，
和
的夹角大小为 
【答案】（1）
．（2）D在AB的中点时．
【解析】
（1）由题意的BO⊥平面ACO，即BO就是三棱锥B﹣ACO的高，然后根据体积建立等式关系，解之即可求出所求；
（2）以O为原点，OA为x轴，OC为y轴，OB为z轴，建立空间直角坐标系，设D（x，0，（1﹣x）），设
和
的夹角为θ，则coaθ
建立等式关系，解之即可求出x的值，从而可判定点D的位置．
（1）由题意的BO⊥平面ACO，即BO就是三棱锥B﹣ACO的高，
在Rt△ABO中，设AO＝a，∠BAO＝60°，所以BO
a，
CO＝a，所以VB﹣ACO
AO×BO×CO
a3．
所以a＝1，所以三棱锥的高BO为．
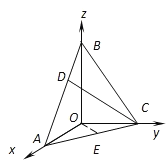
（2）以O为原点，如图建立空间直角坐标系，
设D（x，0，（1﹣x）），则C（0，1，0），E（
，，0 ）
（﹣x，1，（ x﹣1）），
（，，0），
设和的夹角为θ
则coaθ
，
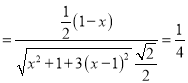解之得，x＝2（舍去）或x
，
所以当D在AB的中点时，和的夹角大小为arccos
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】随着银行业的不断发展，市场竞争越来越激烈，顾客对银行服务质量的要求越来越高，银行为了提高柜员员工的服务意识，加强评价管理，工作中让顾客对服务作出评价，评价分为满意、基本满意、不满意三种．某银行为了比较顾客对男女柜员员工满意度评价的差异，在下属的四个分行中随机抽出40人（男女各半）进行分析比较．对40人一月中的顾客评价“不满意”的次数进行了统计，按男、女分为两组，再将每组柜员员工的月“不满意”次数分为5组：
，
，
，
，
，得到如下频数分布表．
分组 |
|
|
|
|
|
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
（1）在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图；分别求出男、女柜员员工的月平均“不满意”次数的估计值，试根据估计值比较男、女柜员员工的满意度谁高？
（2）在抽取的40名柜员员工中：从“不满意”次数不少于20的员工中随机抽取3人，并用X表示随机抽取的3人中女柜员工的人数，求X的分布列和数学期望．