题目内容
已知二次函数f(x)=ax2+bx+4,集合A={x|f(x)=x}.(1)若A={1},求f(x);
(2)若1∈A,且1≤a≤2,设f(x)在区间
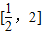 上的最大值、最小值分别为M、m,记g(a)=M-m,求g(a)的最小值.
上的最大值、最小值分别为M、m,记g(a)=M-m,求g(a)的最小值.
【答案】分析:(1)可得ax2+(b-1)x+4=0有两等根为1,故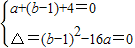 ,解之代入可得;
,解之代入可得;
(2)由题意可得b=-3-a代入解析式配方可得∴f(x)=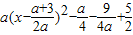 ,结合范围可得M,m,可得g(a),由函数的单调性可得答案.
,结合范围可得M,m,可得g(a),由函数的单调性可得答案.
解答:解:(1)∵A={1},∴ax2+(b-1)x+4=0有两等根为1.…(2分)
∴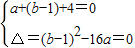 ,解得
,解得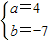 ,
,
∴f(x)=4x2-7x+4.…(4分)
(2)∵1∈A,∴a+(b-1)+4=0,∴b=-3-a.…(5分)
∴f(x)=ax2-(a+3)x+4=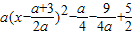 .
.
∵1≤a≤2,∴对称轴为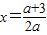
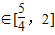 .
.
∵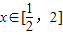 ,∴M=
,∴M=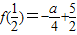 ,m=
,m=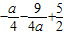 .…(8分)
.…(8分)
∴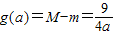 ,由g(a)在[1,2]单调递减
,由g(a)在[1,2]单调递减
可得当a=2时,函数取最小值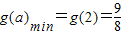 .…(10分)
.…(10分)
点评:本题考查二次函数在闭区间的最值,涉及二次方程与二次函数的关系,以及分式函数的单调性,属中档题.
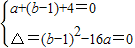 ,解之代入可得;
,解之代入可得;(2)由题意可得b=-3-a代入解析式配方可得∴f(x)=
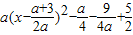 ,结合范围可得M,m,可得g(a),由函数的单调性可得答案.
,结合范围可得M,m,可得g(a),由函数的单调性可得答案.解答:解:(1)∵A={1},∴ax2+(b-1)x+4=0有两等根为1.…(2分)
∴
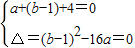 ,解得
,解得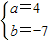 ,
,∴f(x)=4x2-7x+4.…(4分)
(2)∵1∈A,∴a+(b-1)+4=0,∴b=-3-a.…(5分)
∴f(x)=ax2-(a+3)x+4=
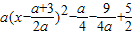 .
.∵1≤a≤2,∴对称轴为
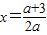
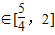 .
.∵
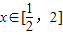 ,∴M=
,∴M=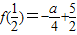 ,m=
,m=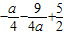 .…(8分)
.…(8分)∴
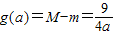 ,由g(a)在[1,2]单调递减
,由g(a)在[1,2]单调递减可得当a=2时,函数取最小值
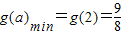 .…(10分)
.…(10分)点评:本题考查二次函数在闭区间的最值,涉及二次方程与二次函数的关系,以及分式函数的单调性,属中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目