题目内容
若关于 的方程
的方程 =0在
=0在 上有解,则
上有解,则 的取值范围是 ( )
的取值范围是 ( )
A. B.
B. C.
C. D.
D.
【答案】
D
【解析】
试题分析:∵x2-x-a-1=0在x∈[-1,1]上有解,∴a=x2-x-1,a′=2x-1,,∴当x∈[-1, ]时函数x2-x-1单调递减,当x∈[
]时函数x2-x-1单调递减,当x∈[ ,1]时函数x2-x-1单调递增,∵当x=-1时,a=1;当x=
,1]时函数x2-x-1单调递增,∵当x=-1时,a=1;当x=
时,a=- 故实数a的范围为[-
故实数a的范围为[- ,1],故答案为D
,1],故答案为D
考点:本题主要是考查方程的根与函数之间的关系.考查根据导函数的正负判断函数的单调性,再由单调性求函数的值域的问题.
点评:解决该试题的关键是先将方程转化为a关于x的二次函数,然后对此函数进行求导运算判断函数在[-1,1]上的单调性,进而求出值域,即为a的取值范围.

练习册系列答案
相关题目
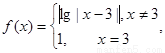 若关于
若关于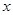 的方程
的方程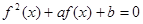 有9个不同实数解,则实数
有9个不同实数解,则实数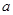 的取值范围是( )
的取值范围是( )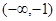
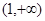 D.
D.
 的方程
的方程 =0在
=0在 上有解,则
上有解,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.