题目内容
设数列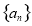 满足:①
满足:①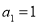 ;②所有项
;②所有项 ;③
;③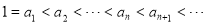 .设集合
.设集合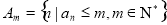 ,将集合
,将集合 中的元素的最大值记为
中的元素的最大值记为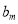 .换句话说,
.换句话说,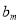 是数列
是数列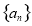 中满足不等式
中满足不等式 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列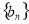 为数列
为数列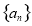 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)请写出数列1,4,7的伴随数列;
(2)设 ,求数列
,求数列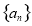 的伴随数列
的伴随数列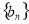 的前
的前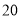 之和;
之和;
(3)若数列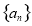 的前
的前 项和
项和 (其中
(其中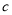 常数),求数列
常数),求数列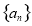 的伴随数列
的伴随数列
的前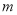 项和
项和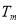 .
.
(1)1,1,1,2,2,2,3;(2)50;(3)
【解析】
试题分析:(1)本题解题的关键是抓住新定义中“ 是数列
是数列 中,满足不等式
中,满足不等式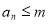 的所有项的项数的最大值”,正确理解题中新定义的内容,根据伴随数列的定义直接写出数列1,4,7的伴随数列;(2)对于这类问题,我们要首先应弄清楚问题的本质,然后根据等差数列、等比数列的性质以及解决数列问题时的常用方法即可解决,根据伴随数列的定义得
的所有项的项数的最大值”,正确理解题中新定义的内容,根据伴随数列的定义直接写出数列1,4,7的伴随数列;(2)对于这类问题,我们要首先应弄清楚问题的本质,然后根据等差数列、等比数列的性质以及解决数列问题时的常用方法即可解决,根据伴随数列的定义得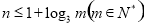 ,由对数的运算对
,由对数的运算对 分类讨论求出伴随数列
分类讨论求出伴随数列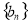 的前20项的和;(3)数列是特殊的函数,以数列为背景是数列的综合问题体现了在知识交汇点上命题的特点,由题意和
的前20项的和;(3)数列是特殊的函数,以数列为背景是数列的综合问题体现了在知识交汇点上命题的特点,由题意和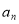 与
与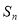 的关系,代入
的关系,代入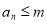 得
得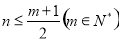 ,求出伴随数列
,求出伴随数列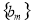 的各项,再对
的各项,再对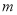 分类讨论得
分类讨论得 .
.
试题解析: 【解析】
(1)由伴随数列的定义得,
数列1,4,7的伴随数列为1,1,1,2,2,2,3(后面加3算对) 5分
(2)由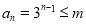 ,得
,得
∴ 当 时,
时, 2分
2分
当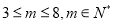 时,
时,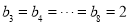 2分
2分
当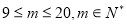 时,
时,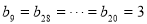 2分
2分
∴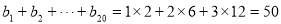 1分
1分
(3)∵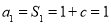 ∴
∴ 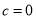 1分
1分
当 时,
时,
∴  1分
1分
由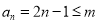 得:
得:
因为使得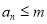 成立的
成立的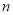 的最大值为
的最大值为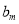 ,
,
所以 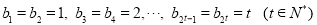 1分
1分
当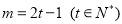 时:
时:
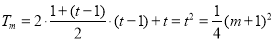 2分
2分
当 时:
时:
 2分
2分
所以 1分
1分
考点:1、新定义求数列;2、数列求和;3、数列的应用.

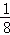 B.
B.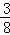 C.
C.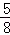 D.
D.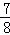
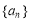 前
前 项和为
项和为 ,则下列一定成立的是
,则下列一定成立的是 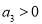 ,则
,则
 ,则
,则
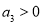 ,则
,则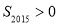
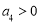 ,则
,则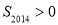
 ”组成一个四位数,则数字“
”组成一个四位数,则数字“ ,若动点
,若动点 在函数
在函数 图象上,则
图象上,则 的最小值为 .
的最小值为 .