题目内容
已知椭圆的中心在坐标原点,以坐标轴为对称轴,且经过两点P1(![]() ,1)、P2(-
,1)、P2(-![]() ,-
,-![]() ),求椭圆方程.
),求椭圆方程.
椭圆方程为![]() +
+![]() =1.
=1.
解析:
设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).
∵P1(![]() ,1)、P2(-
,1)、P2(-![]() ,-
,-![]() )在椭圆上.
)在椭圆上.
∴由题意可知![]() 解得
解得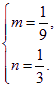
∴椭圆方程为![]() +
+![]() =1.
=1.

练习册系列答案
相关题目
题目内容
已知椭圆的中心在坐标原点,以坐标轴为对称轴,且经过两点P1(![]() ,1)、P2(-
,1)、P2(-![]() ,-
,-![]() ),求椭圆方程.
),求椭圆方程.
椭圆方程为![]() +
+![]() =1.
=1.
设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).
∵P1(![]() ,1)、P2(-
,1)、P2(-![]() ,-
,-![]() )在椭圆上.
)在椭圆上.
∴由题意可知![]() 解得
解得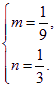
∴椭圆方程为![]() +
+![]() =1.
=1.
